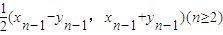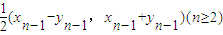已知一非零向量列
{}满足:
=(1,1),
=(xn,yn)=(xn-1-yn-1,xn-1+yn-1) (n≥2)(1)证明:
{||}是等比数列;
(2)设
θn=?-1,> (n≥2),b
n=2nθ
n-1,S
n=b
1+b
2+…+b
n,求S
n.
分析:(1)先利用利用已知条件,利用向量的模的计算求得
||=
|
|,根据等比数列的定义可推断出数列
{||}是以
为首项,公比为
的等比数列
(2)利用向量的基本性质可求得cosθ
n的值,进而求得b
n,最后利用等差数列的求和公式求得答案.
解答:解:(l)∵
||= | (xn-1-yn-1)2+(xn-1+yn-1)2 |
=
=|-1|(n≥2),
又
||=∴数列
{||}是以
为首项,公比为
的等比数列.
(2)∵
-1•=(xn-1•yn-1)•(xn-1-yn-1•xn-1+yn-1)=(+)=|-1|2∴
cosθn==,∴
θn=?-1,>=,∴
bn=2nθn-1=-1Sn=b1+b2++bn=(-1)+(-1)++(-1)=(n2+n)-n 点评:本题主要考查了等比数列的确定.考查了学生对数列基础知识的灵活运用.
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
(2013•成都模拟)已知一非零向量列{a
n}满足:a
1=(1,1),a
n=(x
n,y
n)=
(xn-1-yn-1,xn-1+yn-1)(n≥2)(1)证明:{|a
n|}是等比数列;
(2)设θ
n=<a
n-1,a
n>(n≥2),b
n=2nθ
n-1,S
n=b
1+b
2+…+b
n,求S
n;
(3)设c
n=|a
n|log
2|a
n|,问数列{c
n}中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学
来源:成都一模
题型:解答题
已知一非零向量列{a
n}满足:a
1=(1,1),a
n=(x
n,y
n)=
(xn-1-yn-1,xn-1+yn-1)(n≥2)(1)证明:{|a
n|}是等比数列;
(2)设θ
n=<a
n-1,a
n>(n≥2),b
n=2nθ
n-1,S
n=b
1+b
2+…+b
n,求S
n;
(3)设c
n=|a
n|log
2|a
n|,问数列{c
n}中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学
来源:2012年广东省汕头市高考数学一模试卷(文科)(解析版)
题型:解答题
已知一非零向量列{a
n}满足:a
1=(1,1),a
n=(x
n,y
n)=
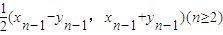
(1)证明:{|a
n|}是等比数列;
(2)设θ
n=<a
n-1,a
n>(n≥2),b
n=2nθ
n-1,S
n=b
1+b
2+…+b
n,求S
n;
(3)设c
n=|a
n|log
2|a
n|,问数列{c
n}中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学
来源:2013年四川省成都市高三12月一诊试卷(理科)(解析版)
题型:解答题
已知一非零向量列{a
n}满足:a
1=(1,1),a
n=(x
n,y
n)=
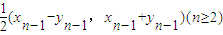
(1)证明:{|a
n|}是等比数列;
(2)设θ
n=<a
n-1,a
n>(n≥2),b
n=2nθ
n-1,S
n=b
1+b
2+…+b
n,求S
n;
(3)设c
n=|a
n|log
2|a
n|,问数列{c
n}中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学
来源:2012年广东省汕头市高三毕业班教学质量检测数学试卷(文科)(解析版)
题型:解答题
已知一非零向量列{a
n}满足:a
1=(1,1),a
n=(x
n,y
n)=

(1)证明:{|a
n|}是等比数列;
(2)设θ
n=<a
n-1,a
n>(n≥2),b
n=2nθ
n-1,S
n=b
1+b
2+…+b
n,求S
n;
(3)设c
n=|a
n|log
2|a
n|,问数列{c
n}中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.
查看答案和解析>>



 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案