
【题目】(12分)如图,底面是正三角形的直三棱柱![]() 中,D是BC的中点,
中,D是BC的中点,![]() .
.
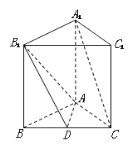
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求的A1 到平面![]() 的距离.
的距离.
【答案】(Ⅰ)参考解析,(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)需证明![]() 平面
平面![]() ,只需要在平面
,只需要在平面![]() 上找到一条直线与
上找到一条直线与![]() 平行,通过三角形的中位线可得以上结论.
平行,通过三角形的中位线可得以上结论.
(Ⅱ)需求点到面的距离,本题通过构建一个三棱锥,让其体积算两次即得到一个等式,即可取出结论.解法一通过三棱锥![]() 与三棱锥
与三棱锥![]() 的体积相等,由体积公式即可求得结论;解法二由(Ⅰ)得到的线面平行转化为三棱锥
的体积相等,由体积公式即可求得结论;解法二由(Ⅰ)得到的线面平行转化为三棱锥![]() 与三棱锥
与三棱锥![]() 体积相等,从而得到结论.
体积相等,从而得到结论.
试题解析:(1)连接![]() 交
交![]() 于O,连接OD,在
于O,连接OD,在![]() 中,O为
中,O为![]() 中点,D为BC中点
中点,D为BC中点
![]() 3分
3分
![]()
![]() 6分
6分

(2)解法一:设![]() 点到平面
点到平面![]() 的距离为h
的距离为h
在![]() 中,
中,![]()
![]()
![]()
![]() 为
为![]()
![]() 8分
8分
![]()
过D作![]() 于H
于H
又![]() 为直棱柱
为直棱柱
![]()
![]() 且
且![]() 10分
10分
![]()
即![]()
解得![]() 12分
12分
解法二:由①可知![]()
![]() 点
点![]() 到平面
到平面![]() 的距离等于点C到平面
的距离等于点C到平面![]() 的距离 8分
的距离 8分
![]() 为
为![]()
![]()
![]() 10分
10分
设点C到面![]() 的距离为h
的距离为h
![]()
即![]()
解得![]() 12分
12分


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知动点
中,已知动点![]() 到定点
到定点![]() 的距离与到定直线
的距离与到定直线![]() 的距离之比为
的距离之比为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知![]() 为定直线
为定直线![]() 上一点.
上一点.
①过点![]() 作
作![]() 的垂线交轨迹
的垂线交轨迹![]() 于点
于点![]() (
(![]() 不在
不在![]() 轴上),求证:直线
轴上),求证:直线![]() 与
与![]() 的斜率之积是定值;
的斜率之积是定值;
②若点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作动直线
作动直线![]() 交轨迹
交轨迹![]() 于不同两点
于不同两点![]() ,线段
,线段![]() 上的点
上的点![]() 满足
满足![]() ,求证:点
,求证:点![]() 恒在一条定直线上.
恒在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,其前n项和为Sn , {bn}是等比数列,且a1=b1=2,a4+b4=27,S4﹣b4=10.
(1)求数列{an}与{bn}的通项公式;
(2)记Tn=anb1+an﹣1b2+…+a1bn , n∈N* , 是否存在实数p,q,r,对于任意n∈N* , 都有Tn=pan+qbn+r,若存在求出p,q,r的值,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的比例 |
第1组 | [18,28) | 5 | 0.5 |
第2组 | [28,38) | 18 | a |
第3组 | [38,48) | 27 | 0.9 |
第4组 | [48,58) | x | 0.36 |
第5组 | [58,68) | 3 | 0.2 |
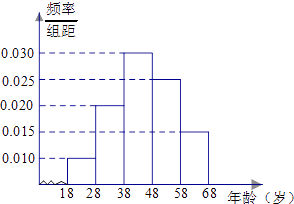
(1)分别求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的增函数,且对于任意的x都有f(﹣x)+f(x)=0恒成立,如果实数a,b满足不等式组 ![]() ,那么a2+b2的取值范围是( )
,那么a2+b2的取值范围是( )
A.[9,49]
B.(17,49]
C.[9,41]
D.(17,41]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com