
分析 将函数f(x)化简后,根据平移变换的规律,得图象关于y轴对称,利用诱导公式可得答案.
解答 解:函数f(x)=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$),向左平移φ个单位,可得$\sqrt{2}$sin(2x+2φ+$\frac{π}{4}$),
要使所得图象关于y轴对称,
∴2φ+$\frac{π}{4}$=$\frac{π}{2}+kπ$,即φ=$\frac{π}{8}+\frac{1}{2}kπ$,(k∈Z)
当k=0时,可得φ的最小正值为$\frac{π}{8}$.
故答案为:$\frac{π}{8}$.
点评 函数y=Asin(ωx+φ)的图象变换规律,诱导公式的运用,属于基础题.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:解答题
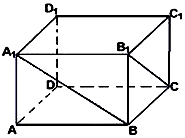 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,4] | B. | [2,+∞) | C. | (2,4) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
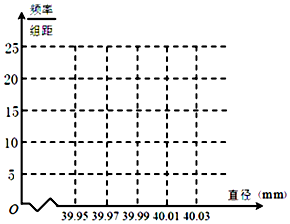 某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
某制造厂商10月份生产了一批乒乓球,从中随机抽取n个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:| 分组 | 频数 | 频率 |
| [39.95,39.97) | 6 | P1 |
| [39.97,39.99) | 12 | 0.20 |
| [39.99,40.01) | a | 0.50 |
| [40.01,40.03) | b | P2 |
| 合计 | n | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14],第二组[14,15),第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14],第二组[14,15),第五组[17,18],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
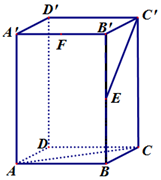 如图长方体ABCD-A'B'C'D'中,AB=BC=1,AA'=2,E、F分别是BB′、A'B'的中点.
如图长方体ABCD-A'B'C'D'中,AB=BC=1,AA'=2,E、F分别是BB′、A'B'的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com