练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

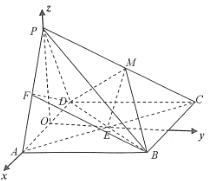
    【题目】如图，四棱锥中，底面是矩形，面底面，且是边长为的等边三角形， 在上，且面.

    （1）求证: 是的中点；

    （2）在上是否存在点，使二面角为直角？若存在，求出的值；若不存在，说明理由.

    【答案】(1) 见解析;(2) .

    【解析】试题分析：(1)连交于可得是中点，再根据面可得进而根据中位线定理可得结果；(2)取中点，由（1）知两两垂直. 以为原点， 所在直线分别为轴, 轴， 轴建立空间直角坐标系，求出面的一个法向量，用表示面的一个法向量，由可得结果.

    试题解析：(1)证明：连交于，连是矩形， 是中点.又面，且是面与面的交线， 是的中点.

    (2)取中点，由（1）知两两垂直. 以为原点， 所在直线分别为轴，

    轴， 轴建立空间直角坐标系（如图），则各点坐标为.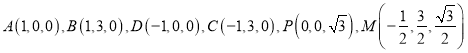

    设存在满足要求，且，则由得： ，面的一个法向量为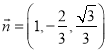，面的一个法向量为，由，得，解得，故存在，使二面角为直角，此时.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知.

    （1）当时，若函数存在与直线平行的切线，求实数的取值范围；

    （2）当时，，若的最小值是，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为调查人们在购物时的支付习惯，某超市对随机抽取的600名顾客的支付方式进行了统计，数据如下表所示：

    支付方式

    微信

    支付宝

    购物卡

    现金

    人数

    200

    150

    150

    100

    现有甲、乙、丙三人将进入该超市购物，各人支付方式相互独立，假设以频率近似代替概率.

    （1）求三人中使用微信支付的人数多于现金支付人数的概率；

    （2）记为三人中使用支付宝支付的人数，求的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）求函数的极值

    （2）定义：若函数在区间 上的取值范围为，则称区间为函数的“美丽区间”．试问函数在上是否存在“美丽区间”？若存在，求出所有符合条件的“美丽区间”；若不存在，请说明理由

    查看答案和解析>>

    科目：高中数学 来源： 题型：

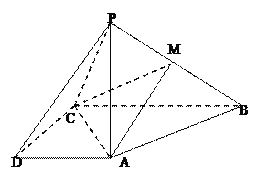
    【题目】如图，在四棱锥中，PA⊥底面ABCD,AD||BC,AD⊥CD，BC=2，AD=CD=1，M是PB的中点．

    （1）求证：AM||平面PCD；

    （2）求证：平面ACM⊥平面PAB；

    （3）若PC与平面ACM所成角为30°，求PA的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】被嘉定著名学者钱大昕赞誉为“国朝算学第一”的清朝数学家梅文鼎曾创造出一类“方灯体”，“灯者立方去其八角也”，如图所示，在棱长为的正方体中，点为棱上的四等分点.

    （1）求该方灯体的体积；

    （2）求直线和的所成角；

    （3）求直线和平面的所成角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】小赵和小王约定在早上至之间到某公交站搭乘公交车去上学，已知在这段时间内，共有班公交车到达该站，到站的时间分别为，，如果他们约定见车就搭乘，则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】.口袋中有质地、大小完全相同的5个球，编号分别为1，2，3，4，5，甲、乙两人玩一种游戏：甲先摸出一个球，记下编号，放回后乙再摸一个球，记下编号，如果两个编号的和为偶数算甲赢，否则算乙赢．

    （Ⅰ）求甲赢且编号的和为6的事件发生的概率；

    （Ⅱ）这种游戏规则公平吗?试说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 的图象过点。

    （1）求的值并求函数的值域；

    （2）若关于的方程有实根，求实数的取值范围；

    （3）若函数， ，则是否存在实数，使得函数的最大值为0？若存在，求出的值；若不存在，请说明理由。

    查看答案和解析>>

    同步练习册答案