
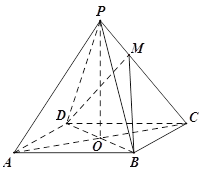
【题目】(本小题满分10分)如图,已知四棱锥![]() 的底面是菱形,对角线
的底面是菱形,对角线![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 底面
底面![]() ,设点
,设点![]() 满足
满足![]() .
.
(1)当![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() 和
和![]() ,圆
,圆![]() 是以
是以![]() 为圆心,半径为
为圆心,半径为![]() 的圆,点
的圆,点![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 所在的直线交于点
所在的直线交于点![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程
的轨迹方程![]() ;
;
(2)已知![]() ,
,![]() 是曲线
是曲线![]() 上的两点,若曲线
上的两点,若曲线![]() 上存在点
上存在点![]() ,满足
,满足![]() (
(![]() 为坐标原点),求实数
为坐标原点),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】足球运动的真谛不仅在于竞技,更在于增强人民体质,培养人们爱国主义、集体主义、顽强拼搏的精神.足球是人类交流的另类“语言”,而其他竞技方式,无论从深度到广度,从速度到力度,都难以与足球比肩,就交流与表达而言,足球是人类最能展露自己天性的运动.
(1)已知某国每年注册足球运动员的人数![]() (万人)与该国年度国际足联排名
(万人)与该国年度国际足联排名![]() 线性相关,统计数据如下表:
线性相关,统计数据如下表:

求变量![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ,并预测该国年度国际足联排名为第
,并预测该国年度国际足联排名为第![]() 时注册足球运动员的人数;(参考公式:
时注册足球运动员的人数;(参考公式: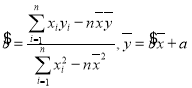 )
)
(参考数据:![]() ;
;![]() )
)
(2)从该国中学生中选出![]() 名男生进行颠球挑战,若能一次性连续颠球超过
名男生进行颠球挑战,若能一次性连续颠球超过![]() 个就可获得一个奖励足球,每人只能挑战一次.已知这
个就可获得一个奖励足球,每人只能挑战一次.已知这![]() 名男生每人能够一次性连续颠球超过
名男生每人能够一次性连续颠球超过![]() 个的概率均为
个的概率均为![]() ,且相互独立.求这
,且相互独立.求这![]() 名男生获得奖励足球个数
名男生获得奖励足球个数![]() 的数学期望
的数学期望![]() 及获得奖励足球超过
及获得奖励足球超过![]() 个的概率(精确到
个的概率(精确到![]() ).(参考数据:
).(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是函数![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )在区间
)在区间![]() 上的图象,为了得到这个函数的图象,只需将
上的图象,为了得到这个函数的图象,只需将![]() (
(![]() )的图像上所有的点( )
)的图像上所有的点( )

A. 向左平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
B. 向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
C. 向左平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
D. 向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 经过椭圆
经过椭圆![]() 的右焦点
的右焦点![]() ,交椭圆
,交椭圆![]() 于点
于点![]() ,
,![]() ,点
,点![]() 为椭圆
为椭圆![]() 的左焦点,
的左焦点,![]() 的周长为
的周长为![]() ..
..
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() 与直线
与直线![]() 的倾斜角互补,且交椭圆
的倾斜角互补,且交椭圆![]() 于点
于点![]() 、
、![]() ,
,![]() ,求证:直线
,求证:直线![]() 与直线
与直线![]() 的交点
的交点![]() 在定直线上.
在定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,直线
,直线![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() 轴的上方).
轴的上方).
(1)若![]() ,求
,求![]() 的面积;
的面积;
(2)是否存在实数![]() 使得以线段
使得以线段![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
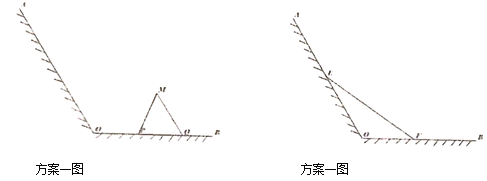
【题目】江心洲有一块如图所示的江边,![]() ,
,![]() 为岸边,岸边形成
为岸边,岸边形成![]() 角,现拟在此江边用围网建一个江水养殖场,有两个方案:方案l:在岸边
角,现拟在此江边用围网建一个江水养殖场,有两个方案:方案l:在岸边![]() 上取两点
上取两点![]() ,用长度为
,用长度为![]() 的围网依托岸边线
的围网依托岸边线![]() 围成三角形
围成三角形![]() (
(![]() ,
,![]() 两边为围网);方案2:在岸边
两边为围网);方案2:在岸边![]() ,
,![]() 上分别取点
上分别取点![]() ,用长度为
,用长度为![]() 的围网
的围网![]() 依托岸边围成三角形
依托岸边围成三角形![]() .请分别计算
.请分别计算![]() ,
,![]() 面积的最大值,并比较哪个方案好.
面积的最大值,并比较哪个方案好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
为回馈顾客,某商场拟通过摸球兑奖的方式对1000位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为50元,其余3个均为10元,求
①顾客所获的奖励额为60元的概率
②顾客所获的奖励额的分布列及数学期望;
(2)商场对奖励总额的预算是60000元,并规定袋中的4个球只能由标有面值10元和50元的两种球组成,或标有面值20元和40元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请对袋中的4个球的面值给出一个合适的设计,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com