
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的左顶点为(﹣2,0),离心率为
=1(a>b>0)的左顶点为(﹣2,0),离心率为 ![]() .
. 
(1)求椭圆C的方程;
(2)已知直线l过点S(4,0),与椭圆C交于P,Q两点,点P关于x轴的对称点为P′,P′与Q两点的连线交x轴于点T,当△PQT的面积最大时,求直线l的方程.
【答案】
(1)解:由题意可得  ,可得c=1,b=
,可得c=1,b= ![]() =
= ![]() .
.
即有椭圆的方程为 ![]() +
+ ![]() =1;
=1;
(2)解:设直线l的方程为x=my+4,P(x1,y1),Q(x2,y2),则P'(x1,﹣y1),
联立 ![]() 得(4+3m2)y2+24my+36=0,
得(4+3m2)y2+24my+36=0,
则△=(24m)2﹣144(4+3m2)=144(m2﹣4)>0,即m2>4.
又y1+y2=﹣ ![]() ,y1y2=
,y1y2= ![]() ,
,
直线PQ的方程为y= ![]() (x﹣x1)﹣y1
(x﹣x1)﹣y1
则xT= ![]() =
= ![]()
= ![]() =
= ![]() +4=1,
+4=1,
则T(1,0),故|ST|=3
所以S△PQT=S△SQT﹣S△SPT= ![]() |y1﹣y2|=
|y1﹣y2|= ![]()
![]() =
= ![]() ,
,
令t= ![]() >0,
>0,
则S△PQT= ![]() =
= ![]() ≤
≤ ![]() =
= ![]() ,
,
当且仅当t2= ![]() 即m2=
即m2= ![]() 即m=±
即m=± ![]() 时取到“=”,
时取到“=”,
故所求直线l的方程为x=± ![]() y+4.
y+4.
【解析】(1)运用椭圆的离心率公式和顶点坐标,以及a,b,c的关系,解得a,b,进而得到椭圆方程;(2)设直线l的方程为x=my+4,P(x1 , y1),Q(x2 , y2),则P'(x1 , ﹣y1),联立直线和椭圆方程,运用韦达定理和判别式大于0,求得直线PQ的方程,令y=0,可得T的横坐标,化简可得T(1,0),由S△PQT=S△SQT﹣S△SPT= ![]() |y1﹣y2|,运用韦达定理,由换元法化简整理运用基本不等式可得最大值,以及此时直线的方程.
|y1﹣y2|,运用韦达定理,由换元法化简整理运用基本不等式可得最大值,以及此时直线的方程.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】甲、乙两人的各科成绩如图中的茎叶图所示,则下列说法不正确的是( )

A. 甲、乙两人的各科平均分相同
B. 甲各科成绩的中位数是83,乙各科成绩的中位数是85
C. 甲各科成绩比乙各科成绩稳定
D. 甲各科成绩的众数是89,乙各科成绩的众数为87
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某礼品店要制作一批长方体包装盒,材料是边长为![]() 的正方形纸板.如图所示,先在其中相邻两个角处各切去一个边长是
的正方形纸板.如图所示,先在其中相邻两个角处各切去一个边长是![]() 的正方形,然后在余下两个角处各切去一个长、宽分别为
的正方形,然后在余下两个角处各切去一个长、宽分别为![]() 、
、![]() 的矩形,再将剩余部分沿图中的虚线折起,做成一个有盖的长方体包装盒.
的矩形,再将剩余部分沿图中的虚线折起,做成一个有盖的长方体包装盒.

(1)求包装盒的容积![]() 关于
关于![]() 的函数表达式,并求函数的定义域;
的函数表达式,并求函数的定义域;
(2)当![]() 为多少时,包装盒的容积最大?最大容积是多少?
为多少时,包装盒的容积最大?最大容积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①若![]() ,
, ![]() 是第一象限角且
是第一象限角且![]() ,则
,则![]() ;
;
②函数![]() 在
在![]() 上是减函数;
上是减函数;
③![]() 是函数
是函数![]() 的一条对称轴;
的一条对称轴;
④函数![]() 的图象关于点
的图象关于点![]() 成中心对称;
成中心对称;
⑤设![]() ,则函数
,则函数![]() 的最小值是
的最小值是![]() ,其中正确命题的序号为 __________.
,其中正确命题的序号为 __________.
查看答案和解析>>
科目:高中数学 来源: 题型:
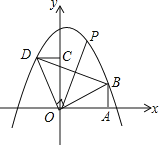
【题目】如图所示,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到![]() ,抛物线
,抛物线![]() 经过B、D两点.
经过B、D两点.
(1)求二次函数的解析式;
(2)连接BD,点P是抛物线上一点,直线OP把△BOD的周长分成相等的两部分,求点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车站每天均有3辆开往省城的分为上、中、下等级的客车,某天袁先生准备在该汽车站乘车前往省城办事,但他不知道客车的车况,也不知道发车顺序.为了尽可能乘上上等车,他采取如下策略:先放过一辆,如果第二辆比第一辆好则上第二辆,否则上第三辆.则他乘上上等车的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后抛掷两枚骰子,设出现的点数之和是12,11,10的概率依次是P1,P2,P3,则( )
(A)P1=P2<P3 (B)P1<P2<P3 (C)P1<P2=P3 (D)P3=P2<P1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com