
 b=ab2+a2b,则sin15°
b=ab2+a2b,则sin15° cos15°的值是 .
cos15°的值是 .  cos15°,然后利用二倍角公式及两角和的正弦函数公式化简,再利用特殊角的三角函数值得到即可.
cos15°,然后利用二倍角公式及两角和的正弦函数公式化简,再利用特殊角的三角函数值得到即可. cos15°=sin15°cos215°+sin215°cos15°
cos15°=sin15°cos215°+sin215°cos15° ×2sin15°cos15°(sin45°cos15°+cos45°sin15°)
×2sin15°cos15°(sin45°cos15°+cos45°sin15°) sin30°sin(15°+45°)=
sin30°sin(15°+45°)= .
.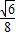


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com