
分析 (1)先求出C的直角坐标方程,再求曲线C的参数方程;
(2)利用C的参数方程,结合三角函数知识,求x+y的最大值,并求此时点M的直角坐标.
解答 解:(1)由曲线C的方程为$ρ=4(cosθ+sinθ)-\frac{6}{ρ}$,得ρ2=4ρcosθ+4ρsinθ-6,
即x2+y2-4x-4y+6=0,即(x-2)2+(y-2)2=2.
即曲线C是以点为圆心(2,2),以$\sqrt{2}$为半径的圆,
则圆的参数方程为$\left\{\begin{array}{l}{x=2+\sqrt{2}cosθ}\\{y=2+\sqrt{2}sinθ}\end{array}\right.$(θ为参数).
(2)x+y=4+$\sqrt{2}$cosθ+$\sqrt{2}$sinθ=4+2sin(θ+$\frac{π}{4}$).
于是当θ=$\frac{π}{4}$时,(x+y)max=4+2=6,
此时$\left\{{\begin{array}{l}{x=2+\sqrt{2}cos\frac{π}{4}=3}\\{y=2+\sqrt{2}sin\frac{π}{4}=3}\end{array}}\right.$,即M(3,3).
点评 本题考查三种方程的互化,考查参数方程的运用,考查三角函数知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
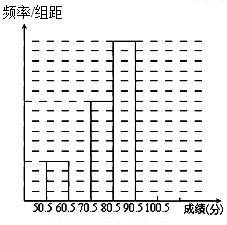 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 6 | 0.08 |
| 60.5~70.5 | 12 | 0.16 |
| 70.5~80.5 | 15 | 0.2 |
| 80.5~90.5 | 24 | 0.32 |
| 90.5~100.5 | 18 | 0.24 |
| 合计 | 75 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
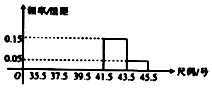 某商场为了了解某日旅游鞋的销售情况,抽取了部分顾客所购鞋的尺寸,将所得数据整理后,画出频率分布直方图如图所示.已知从左到右前3个小组的频率之比为1:2:3,第4小组与第5小组的频率分布如图所示,第2小组的频数为10,则第4小组顾客的人数是( )
某商场为了了解某日旅游鞋的销售情况,抽取了部分顾客所购鞋的尺寸,将所得数据整理后,画出频率分布直方图如图所示.已知从左到右前3个小组的频率之比为1:2:3,第4小组与第5小组的频率分布如图所示,第2小组的频数为10,则第4小组顾客的人数是( )| A. | 15 | B. | 20 | C. | 25 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{21}{8}$ | B. | $\frac{21}{8}$ | C. | -9 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com