练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．下列说法正确的是（　　）
    A．直线的倾斜角的取值范围是[0°，180°]
    B．若直线的倾斜角为90°，则这条直线与y轴平行
    C．任意一条直线都有倾斜角和斜率
    D．若直线l的倾斜角为锐角，则它的斜率大于0；若直线l的倾斜角为钝角，则它的斜率小于0

    分析 A，直线的倾斜角的取值范围是[0°，180°）；
    B，直线的倾斜角为90°，这条直线与y轴平行或重合；
    C，直线都的倾斜角为900时无斜率；
    D，当倾斜角θ≠900时，直线的斜率k=tanθ，由正切函数的性质可判定，

    解答 解：对于A，直线的倾斜角的取值范围是[0°，180°），故错；
    对于B，若直线的倾斜角为90°，则这条直线与y轴平行或重合，故错；
    对于C，直线都的倾斜角为900时无斜率，故错；
    对于D，当倾斜角θ≠900时，直线的斜率k=tanθ，由正切函数的性质可判定，直线l的倾斜角为锐角，
    则它的斜率大于0；若直线l的倾斜角为钝角，则它的斜率小于0，故正确．
    故选：D．

    点评 本题考查了直线的倾斜角、斜率的定义及性质，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

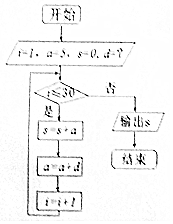    2．《九章算术》之后，人们学会了用数列的知识来解决问题．公元5世纪中国古代内容丰富的数学著作《张丘建算经》卷上有题为：“今有女善织，日益功疾，初日织五尺，今一月织九匹三丈．问日益几何？”．利用这种思想设计的一个程序框图如图，若输出的S值为九匹三丈（一匹=4丈，一丈=10尺），则框图中d为（　　）
    A．$\frac{1}{2}$尺B．$\frac{8}{15}$尺C．$\frac{16}{31}$尺D．$\frac{16}{29}$尺

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．为了得到函数y=sin（2x-$\frac{π}{3}$）的图象，只需将函数y=sin2x的图象上所有的点（　　）
    A．向左平移$\frac{π}{6}$个单位B．向左平移$\frac{π}{3}$个单位
    C．向右平移$\frac{π}{6}$个单位D．向右平移$\frac{π}{3}$个单位

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知f（x）=x2+2xf′（-1），则f′（0）等于（　　）
    A．4B．0C．-2D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

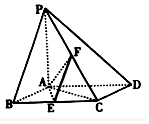    1．如图，已知四棱锥P-ABCD，地面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．
    （1）证明：AE⊥PD；
    （Ⅱ）若AB=2，PA=2，求四面体P-AEF的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知$\overrightarrow{a}$=（1，2，-y），$\overrightarrow{b}$=（x，1，2），且（$\overrightarrow{a}$+2$\overrightarrow{b}$）∥（2$\overrightarrow{a}$-$\overrightarrow{b}$），则x+y=$\frac{7}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知三棱锥P-ABC的四个顶点P，A，B，C都在半径为R的同一个球面上，若PA，PB，PC两两相互垂直，且PA=1，PB=2，PC=3，则R等于（　　）
    A．$\frac{{\sqrt{14}}}{2}$B．$\sqrt{14}$C．$\frac{{\sqrt{13}}}{2}$D．$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知向量$\overrightarrow a=（{m，1}），\overrightarrow b=（{1，n-2}），（{m＞0，n＞0}）$若$\overrightarrow a⊥\overrightarrow b$，则$\frac{1}{m}+\frac{2}{n}$的最小值为（　　）
    A．2$\sqrt{2}$B．$\frac{3}{2}$+$\sqrt{2}$C．3$\sqrt{2}$+2D．2$\sqrt{2}$+3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

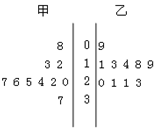    16．某篮球队甲、乙两名运动员练习罚球，每人练习10组，每组罚球40个，命中个数的茎叶图如图所示，则下列结论错误 的一个是（　　）
    A．甲的极差是29B．甲的中位数是25
    C．乙的众数是21D．甲的平均数比乙的大

    查看答案和解析>>

    同步练习册答案