Question

某车间生产一种机器的两种配件A和B，已知生产配件A的成本费用与该车间的工人人数成反比，而生产配件B的成本费用又与该车间的工人人数成正比；且当该车间的工人人数为10人时，这两项费用分别为2万元和8万元．现在要使这两项费用之和最小，则该车间的工人人数应为多少？

Answer 1

解：由题意，设
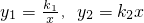
∵该车间的工人人数为10人时，这两项费用分别为2万元和8万元
∴
∴
∴，
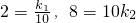
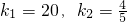
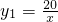
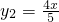
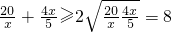
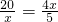
设两项费用之和为y，则y=y₁+y₂=，当且仅当，即x=5时，等号成立，
答：当车间的工人人数为5人时，两项费用之和最少．
分析：根据当该车间的工人人数为10人时，这两项费用分别为2万元和8万元，求出两项费用的函数关系式，再利用基本不等式，即可求得结论．
点评：本题考查函数模型的构建，考查基本不等式的运用，属于中档题．