
设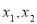
 是函数
是函数 (
( )的两个极值点
)的两个极值点
(1)若 ,求函数
,求函数 的解析式;
的解析式;
(2)若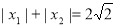 ,求
,求 的最大值。
的最大值。
(1)  ;(2)4
;(2)4
【解析】
试题分析:(1)求出f′(x),因为x1、x2是函数f(x)的两个极值点,而x1=-1,x2=2所以得到f′(-1)=0,f′(2)=0代入求出a、b即可得到函数解析式;
(2)因为x1、x2是导函数f′(x)=0的两个根,利用根与系数的关系对已知进行变形得到a和b的等式,求出b的范围,设h(a)=3a2(6-a),求出其导函数,利用导数研究函数的增减性得到h(a)=的极大值,开方可得b的最大值.
试题解析:
(1)∵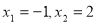 是函数
是函数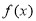 的极值点,
的极值点,
∴ ∴
∴ 4分
4分
(2) 中
中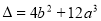 对
对
∴ 的两个不相等的实根
的两个不相等的实根
由韦达定理知 ,
,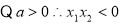 6分
6分
∴|x1|+|x2|=|x1-x2|= 8分
8分
∴ 即
即 9分
9分
令
 ;
;
 11分
11分
 ∴b≤4
∴b≤4 12分
12分
考点:导数在函数中的应用.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源:2015届北京东城(南片)高二上学期期末考试文数学试卷(解析版) 题型:选择题
已知正方形ABCD,AB=2,AC、BD交点为O,在ABCD内随机取一点E,则点E满足OE<1的概率为
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2015届北京东城区高二第一学期期末考试文科数学试卷(解析版) 题型:选择题
“ ”是“直线
”是“直线 相切”的( )
相切”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届云南玉溪一中高二上学期期末考试理科数学试卷(解析版) 题型:选择题
已知 ,
, ,则
,则 是
是 成立的 ( )
成立的 ( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习真题感悟常考问题1练习卷(解析版) 题型:选择题
函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=ex关于y轴对称,则f(x)= ( ).
A.ex+1 B.ex-1 C.e-x+1 D.e-x-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com