
【题目】已知a∈R,函数f(x)= ![]() +alnx﹣3x,g(x)=﹣x2+8x,且x=1是函数f(x)的极大值点.
+alnx﹣3x,g(x)=﹣x2+8x,且x=1是函数f(x)的极大值点.
(1)求a的值.
(2)如果函数y=f(x)和函数y=g(x)在区间(b,b+1)上均为增函数,求实数b的取值范围.
【答案】
(1)解:因为函数 ![]() (x>0)
(x>0)
所以f′(x)=x+ ![]() ﹣3,(x>0),
﹣3,(x>0),
又因为x=1是函数f(x)的极大值点.
所以 ![]() ,解得a=2
,解得a=2
检验:当a=2时, ![]() (x>0)
(x>0)
当x∈(0,1),(2,+∞)时,f′(x)>0,当x∈(1,2)时,f′(x)<0,
所以x=1是函数f(x)的极大值点,a=2符合题意
(2)解:g(x)=﹣x2+8x=﹣(x﹣4)2+16
所以函数g(x)的单调递增区间是(4,+∞)
又由(1)可知函数f(x)的单调递增区间是(0,1),(2,+∞)
所以依题意得 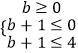 或
或 ![]()
解得 b=0或 2≤b≤3
所以实数b的取值范围是{0}∪[2,3]
【解析】(1)因为函数 ![]() (x>0),求出导函数,利用x=1是函数f(x)的极大值点.求出a.然后验证即可.(2)求出函数g(x)的单调递增区间.又由(1)可知函数f(x)的单调递增区间是(0,1),(2,+∞),列出不等式组,求解b 的范围即可.
(x>0),求出导函数,利用x=1是函数f(x)的极大值点.求出a.然后验证即可.(2)求出函数g(x)的单调递增区间.又由(1)可知函数f(x)的单调递增区间是(0,1),(2,+∞),列出不等式组,求解b 的范围即可.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知常数![]() ,在矩形ABCD中,
,在矩形ABCD中, ![]() ,
, ![]() ,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且
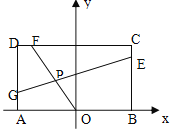
,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且![]() ,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由
,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x+a=0上存在两点关于直线l:mx+y+1=0对称. (Ⅰ)求m的值;
(Ⅱ)直线l与圆C交于A,B两点, ![]()
![]() =﹣3(O为坐标原点),求圆C的方程.
=﹣3(O为坐标原点),求圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查了解某省属师范大学师范类毕业生参加工作后,从事的工作与教育是否有关的情况,该校随机调查了该校80位性别不同的2016年师范类毕业大学生,得到具体数据如下表:
与教育有关 | 与教育无关 | 合计 | |
男 | 30 | 10 | 40 |
女 | 35 | 5 | 40 |
合计 | 65 | 15 | 80 |
(1)能否在犯错误的概率不超过5%的前提下,认为“师范类毕业生从事与教育有关的工作与性别有关”?
参考公式:![]() (
(![]() ).
).
附表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.023 | 6.635 |
(2)求这80位师范类毕业生从事与教育有关工作的频率;
(3)以(2)中的频率作为概率.该校近几年毕业的2000名师范类大学生中随机选取4名,记这4名毕业生从事与教育有关的人数为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在(﹣1,+∞)内的增函数,且f(xy)=f(x)+f(y)若f(3)=1且f(a)>f(a﹣1)+2
求:
(1)f(9)的值,
(2)求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com