
【题目】已知等差数列{an}的前n项和为Sn , 且a1+a3=10,S4=24.
(1)求数列{an}的通项公式;
(2)令Tn= ![]() ,求证:Tn<
,求证:Tn< ![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】
如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,AC=16,PA=PC=10.
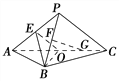
(Ⅰ)设G是OC的中点,证明:FG∥平面BOE;
(Ⅱ)证明:在△ABO内存在一点M,使FM⊥平面BOE,并求点M到OA,OB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某几何体的三视图中,俯视图是边长为2的正三角形,正视图和左视图分别为直角梯形和直角三角形,则该几何体的体积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某几何体的三视图中,俯视图是边长为2的正三角形,正视图和左视图分别为直角梯形和直角三角形,则该几何体的体积为( )
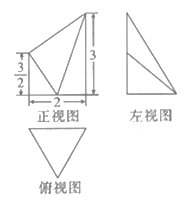
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M,N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S﹣ABCD的体积为V(x),则函数V(x)的图象是( ) 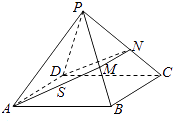
A.
B.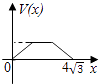
C.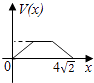
D.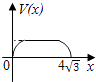
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,设不等式组 ![]() 所表示的平面区域是W,从区域W中随机取点M(x,y).
所表示的平面区域是W,从区域W中随机取点M(x,y).
(1)若x,y∈Z,求点M位于第一象限的概率;
(2)若x,y∈R,求|OM|≥1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,如果存在正实数
,如果存在正实数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,且
,且![]() 恒成立,则称函数
恒成立,则称函数![]() 为
为![]() 上的“
上的“![]() 的型增函数”,已知
的型增函数”,已知![]() 是定义在
是定义在![]() 上的奇函数,且在
上的奇函数,且在![]() 时,
时, ![]() ,若
,若![]() 为
为![]() 上的“2017的型增函数”,则实数
上的“2017的型增函数”,则实数![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com