
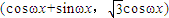 ,n=(cosωx-sinωx,2sinωx),其中ω>0,若函数f(x)=m•n,且f(x)的对称中心到f(x)对称轴的最近距离不小于
,n=(cosωx-sinωx,2sinωx),其中ω>0,若函数f(x)=m•n,且f(x)的对称中心到f(x)对称轴的最近距离不小于
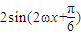 ,由于函数f(x)的周期
,由于函数f(x)的周期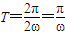 ,由题意知
,由题意知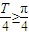 ,即
,即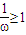 ,又ω>0,从而可确定ω的取值范围;
,又ω>0,从而可确定ω的取值范围;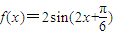 .利用f(A)=1,可求
.利用f(A)=1,可求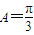 .由余弦定理可知:
.由余弦定理可知: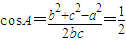 ,∴b2+c2-bc=1,又b+c=2,从而可求得:
,∴b2+c2-bc=1,又b+c=2,从而可求得: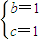 或
或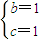 ,故可求△ABC的面积.
,故可求△ABC的面积.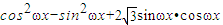 =
=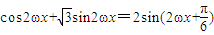 (3分)∵ω>0,∴函数f(x)的周期
(3分)∵ω>0,∴函数f(x)的周期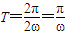 ,由题意知
,由题意知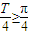 ,即
,即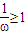 ,
, .
. .而
.而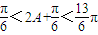 ,∴
,∴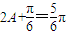 ,∴
,∴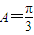 . (9分)
. (9分)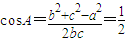 ,∴b2+c2-bc=1,又b+c=2.联立解得:
,∴b2+c2-bc=1,又b+c=2.联立解得: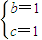 或
或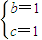 .
.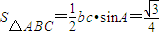 .(13分)
.(13分)

科目:高中数学 来源: 题型:
| 3 |
| AC |
| CO |
| AC |
| CO |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| α |
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| AP |
| AO |
| AC |
| PA |
| PB |
| PC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com