
分析 (Ⅰ)把x=$\frac{π}{4}$代入函数解析式可求得m的值,进而根据函数为奇函数推断出f(0)=0,进而求得cosθ,则θ的值可得函数解析式,进而可得函数f(x)的图象的对称中心和单调递增区间
(Ⅱ)由f($\frac{C}{2}$+$\frac{π}{24}$)=-$\frac{1}{2}$可得C角,结合余弦定理及c=1,ab=2$\sqrt{3}$,可得△ABC的周长.
解答 解:(Ⅰ)f($\frac{π}{4}$)=-(m+1)sinθ=0,
∵θ∈(0,π).
∴sinθ≠0,
∴m+1=0,即m=-1,
∵f(x)为奇函数,
∴f(0)=(m+2)cosθ=0,
∴cosθ=0,θ=$\frac{π}{2}$.
故f(x)=(-1+2cos2x)cos(2x+$\frac{π}{2}$)=cos2x•(-sin2x)=-$\frac{1}{2}$sin4x,
由4x=kπ,k∈Z得:x=$\frac{1}{4}$kπ,k∈Z,
故函数f(x)的图象的对称中心坐标为:($\frac{1}{4}$kπ,0),k∈Z,
由4x∈[$\frac{π}{2}$+2kπ,$\frac{3π}{2}$+2kπ],k∈Z得:x∈[$\frac{π}{8}$+$\frac{1}{2}$kπ,$\frac{3π}{8}$+$\frac{1}{2}$kπ],k∈Z,
即函数f(x)的单调递增区间为[$\frac{π}{8}$+$\frac{1}{2}$kπ,$\frac{3π}{8}$+$\frac{1}{2}$kπ],k∈Z,
(Ⅱ)∵f($\frac{C}{2}$+$\frac{π}{24}$)=-$\frac{1}{2}$sin(2C+$\frac{π}{6}$)-$\frac{1}{2}$,C为三角形内角,
故C=$\frac{π}{6}$,
∴c2=a2+b2-2abcosC=${a}^{2}+{b}^{2}-\sqrt{3}ab$=${(a+b)}^{2}-(2+\sqrt{3})ab$,
∵c=1,ab=2$\sqrt{3}$,
∴a+b=2+$\sqrt{3}$,
∴a+b+c=3+$\sqrt{3}$,
即△ABC的周长为3+$\sqrt{3}$.
点评 本题主要考查了同角三角函数关系,三角函数恒等变换的应用,函数奇偶性问题.综合运用了所学知识解决问题的能力.


科目:高中数学 来源: 题型:选择题
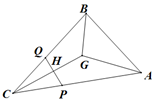 如图,在△ABC中,$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$,$\overrightarrow{CA}$=$\overrightarrow{a}$,$\overrightarrow{CB}$=$\overrightarrow{b}$,已知点P,Q分别为线段CA,CB(不含端点)上的动点,PQ与CG交于H,且H为线段CG中点,若$\overrightarrow{CP}$=m$\overrightarrow{a}$,$\overrightarrow{CQ}$=n$\overrightarrow{b}$,则$\frac{1}{m}$+$\frac{1}{n}$=( )
如图,在△ABC中,$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$,$\overrightarrow{CA}$=$\overrightarrow{a}$,$\overrightarrow{CB}$=$\overrightarrow{b}$,已知点P,Q分别为线段CA,CB(不含端点)上的动点,PQ与CG交于H,且H为线段CG中点,若$\overrightarrow{CP}$=m$\overrightarrow{a}$,$\overrightarrow{CQ}$=n$\overrightarrow{b}$,则$\frac{1}{m}$+$\frac{1}{n}$=( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=x+\frac{1}{x}$ | B. | $f(x)=\frac{1}{x^2}$ | ||
| C. | $f(x)=\sqrt{{x^2}-1}+\sqrt{1-{x^2}}$ | D. | $f(x)=\left\{\begin{array}{l}\frac{1}{2}{x^2}+1,x>0\\-\frac{1}{2}{x^2}-1,x<0\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
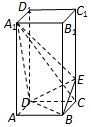 如图,在长方体ABCD-A1B1C1B1中,AA1=2AB=2AD=4,点E在CC1上且C1E=3EC.利用空间向量解决下列问题:
如图,在长方体ABCD-A1B1C1B1中,AA1=2AB=2AD=4,点E在CC1上且C1E=3EC.利用空间向量解决下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,长方体ABCD-A1B1C1D1中,D1D=DC=4,AD=2,E为D1C的中点.
如图,长方体ABCD-A1B1C1D1中,D1D=DC=4,AD=2,E为D1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | -$\frac{π}{3}$ | $\frac{2π}{3}$ | $\frac{5π}{3}$ | $\frac{8π}{3}$ | $\frac{11π}{3}$ |
| $\frac{1}{2}x+\frac{π}{6}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| y | 0 | 2 | 0 | -2 | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com