
【题目】数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列,![]() ,
,![]() ;数列
;数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() .
.
(1)求![]() ,
,![]() ;
;
(2)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(3)求![]() .
.
【答案】(1)1,5;(2)![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据题意,可知数列![]() 满足
满足![]() ,令
,令![]() 和
和![]() 时,代入计算,即可求出
时,代入计算,即可求出![]() ,
,![]() ;
;
(2)运用等比数列的通项公式求出基本量,即可求出![]() 的通项公式;根据
的通项公式;根据![]() 和
和![]() 的关系和递推关系,利用等差中项法证明
的关系和递推关系,利用等差中项法证明![]() 是首项为
是首项为![]() ,公差
,公差![]() 的等差数列,即可求出
的等差数列,即可求出![]() 的通项公式;
的通项公式;
(3)由(2)得出![]() ,运用数列的错位相减法求和,结合等比数列的求和公式,计算可得所求结果.
,运用数列的错位相减法求和,结合等比数列的求和公式,计算可得所求结果.
解:(1)由于数列![]() 满足
满足![]() ,
,![]() ,
,
则![]() ,解得:
,解得:![]() ,
,
![]() ,解得:
,解得:![]() .
.
(2)由题可知,等比数列![]() 的公比为正数,即
的公比为正数,即![]() ,
,
且![]() ,
,![]()
易知![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
则![]() ,故
,故![]() ,
,![]() ;
;
由于![]() ,①
,①
则![]() ,
,![]() ,②
,②
①-②得:![]() ,③
,③
则有:![]() ,
,![]() ,④
,④
同理③-④得:![]() ,
,![]() (注
(注![]() ,
,![]() 也符合),
也符合),
则![]() 为等差数列,首项
为等差数列,首项![]() ,公差
,公差![]() ,
,
故![]() ,
,![]() .
.
(3)由(2)得出![]() ,
,
设![]() ,
,
则![]() ,
,
![]() ,
,
两式相减可得:![]() ,
,
即![]() ,
,
化简可得![]() ,
,
即![]() .
.


科目:高中数学 来源: 题型:
【题目】有2名男生、3名女生,全体排成一行,问下列情形各有多少种不同的排法?(以下各题请用数字作答)
(1)甲不在中间也不在两端;
(2)甲、乙两人必须排在两端;
(3)男、女生分别排在一起;
(4)男女相间;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网购是当前民众购物的新方式,某公司为改进营销方式,随机调査了100名市民,统计其周平均网购
的次数,并整理得到如右的频数直方图,将周平均网购次数不小于4次的民众称为网购迷.这100名市民中,年龄不超过40岁的有65人,且网购迷中有5名市民的年龄超过40岁
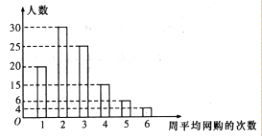
(1)根据已知条件完成下面的2×2列联表,能否在犯错误的概率不超过0.10的前提条件下认为网购迷与年龄不超过40岁有关?
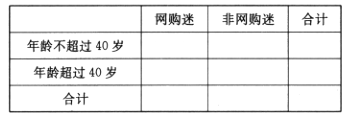
(2)现从网购迷中按分层抽样选5人代表进一步进行调查,若从5人代表中任意挑选2人,求挑选的2人中有年龄超过40岁的概率

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司共有10条产品生产线,不超过5条生产线正常工作时,每条生产线每天纯利润为1100元,超过5条生产线正确工作时,超过的生产线每条纯利润为800元,原生产线利润保持不变.未开工的生产线每条每天的保养等各种费用共100元.用x表示每天正常工作的生产线条数,用y表示公司每天的纯利润.
(I)写出y关于x的函数关系式,并求出纯利润为7700元时工作的生产线条数.
(II)为保证新开的生产线正常工作,需对新开的生产线进行检测,现从该生产线上随机抽取100件产品,测量产品数据,用统计方法得到样本的平均数![]() ,标准差
,标准差![]() ,绘制如图所示的频率分布直方图,以频率值作为概率估计值.为检测该生产线生产状况,现从加工的产品中任意抽取一件,记其数据为X,依据以下不等式评判(P表示对应事件的概率)
,绘制如图所示的频率分布直方图,以频率值作为概率估计值.为检测该生产线生产状况,现从加工的产品中任意抽取一件,记其数据为X,依据以下不等式评判(P表示对应事件的概率)
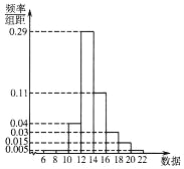
①![]()
②![]()
③![]()
评判规则为:若至少满足以上两个不等式,则生产状况为优,无需检修;否则需检修生产线.试判断该生产线是否需要检修.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一工厂生产了某种产品700件,该工厂需要对这些产品的性能进行检测现决定利用随机数表法从中抽取100件产品进行抽样检测,将700件产品按001,002,…,700进行编号
(1)如果从第8行第4列的数开始向右读,请你依次写出最先检测的3件产品的编号;(下面摘取了随机数表的第7~9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)检测结果分为优等、合格、不合格三个等级,抽取的100件产品的安全性能和环保性能的检测结果如下表(横向和纵向分别表示安全性能和环保性能):
(i)若在该样本中,产品环保性能是优等的概率为34%,求![]() 的值;
的值;
(ii)若![]() ,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率.
,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率.
件数 | 环保性能 | |||
优等 | 合格 | 不合格 | ||
安全性能 | 优等 | 6 | 20 | 5 |
合格 | 10 | 18 | 6 | |
不合格 | m | 4 | n | |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块半圆形的空地,直径![]() 米,政府计划在空地上建一个形状为等腰梯形的花圃
米,政府计划在空地上建一个形状为等腰梯形的花圃![]() ,如图所示,其中
,如图所示,其中![]() 为圆心,
为圆心,![]() ,
,![]() 在半圆上,其余为绿化部分,设
在半圆上,其余为绿化部分,设![]() .
.

(1)记花圃的面积为![]() ,求
,求![]() 的最大值;
的最大值;
(2)若花圃的造价为10元/米,在花圃的边![]() 、
、![]() 处铺设具有美化效果的灌溉管道,铺设费用为500元/米,两腰
处铺设具有美化效果的灌溉管道,铺设费用为500元/米,两腰![]() 、
、![]() 不铺设,求
不铺设,求![]() 满足什么条件时,会使总造价最大.
满足什么条件时,会使总造价最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2019·潍坊期末]某钢铁加工厂新生产一批钢管,为了了解这批产品的质量状况,检验员随机抽取了100件钢管作为样本进行检测,将它们的内径尺寸作为质量指标值,由检测结果得如下频率分布表和频率分布直方图:
分组 | 频数 | 频率 |
25.05~25.15 | 2 | 0.02 |
25.15~25.25 | ||
25.25~25.35 | 18 | |
25.35~25.45 | ||
25.45~25.55 | ||
25.55~25.65 | 10 | 0.1 |
25.65~25.75 | 3 | 0.03 |
合计 | 100 | 1 |
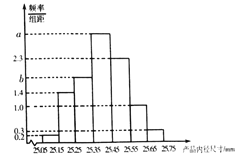
(1)求![]() ,
,![]() ;
;
(2)根据质量标准规定:钢管内径尺寸大于等于25.75或小于25.15为不合格,钢管尺寸在![]() 或
或![]() 为合格等级,钢管尺寸在
为合格等级,钢管尺寸在![]() 为优秀等级,钢管的检测费用为0.5元/根.
为优秀等级,钢管的检测费用为0.5元/根.
(i)若从![]() 和
和![]() 的5件样品中随机抽取2根,求至少有一根钢管为合格的概率;
的5件样品中随机抽取2根,求至少有一根钢管为合格的概率;
(ii)若这批钢管共有2000根,把样本的频率作为这批钢管的频率,有两种销售方案:
①对该批剩余钢管不再进行检测,所有钢管均以45元/根售出;
②对该批剩余钢管一一进行检测,不合格产品不销售,合格等级的钢管50元/根,优等钢管60元/根.
请你为该企业选择最好的销售方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com