
【题目】已知函数![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)设![]() ,证明:当
,证明:当![]() 时,
时,![]() ;
;
(Ⅲ)设![]() 是
是![]() 的两个零点,证明
的两个零点,证明![]() .
.
【答案】(Ⅰ)![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;(Ⅱ)当
上单调递增;(Ⅱ)当![]() 时,
时,![]() ;(Ⅲ)证明过程见解析
;(Ⅲ)证明过程见解析
【解析】试题分析:(Ⅰ)求导,并判断导数的符号,分别讨论![]() 的取值,确定函数的单调区间.
的取值,确定函数的单调区间.
(Ⅱ)构造函数![]() ,利用导数求函数
,利用导数求函数![]() 当
当![]() 时的最大值小于零即可.
时的最大值小于零即可.
(Ⅲ)由(Ⅱ)得![]() ,从而
,从而![]() ,于是
,于是![]() ,由(Ⅰ)知,
,由(Ⅰ)知,![]() .
.
试题解析:(Ⅰ)![]() 的定义域为
的定义域为![]() ,
,
求导数,得![]() ,
,
若![]() ,则
,则![]() ,此时
,此时![]() 在
在![]() 上单调递增,
上单调递增,
若![]() ,则由
,则由![]() 得
得![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
此时![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(Ⅱ)令![]() ,则
,则

![]() .
.
求导数,得![]() ,
,
当时![]() ,
,![]() ,
,![]() 在
在![]() 上是减函数.
上是减函数.
而![]() ,
,![]() ,
,
故当![]() 时,
时,![]()
(Ⅲ)由(Ⅰ)可知,当![]() 时,函数
时,函数![]() 至多有一个零点,
至多有一个零点,
故![]() ,从而
,从而![]() 的最小值为
的最小值为![]() ,且
,且![]() ,
,
不妨设![]() ,则
,则![]() ,
,![]() ,
,
由(Ⅱ)得![]() ,
,
从而![]() ,于是
,于是![]() ,
,
由(Ⅰ)知,![]() .
.
点晴:本题考查函数导数的单调性.不等式比较大小,函数的零点问题:在(Ⅰ)中通过求导,并判断导数的符号,分别讨论![]() 的取值,确定函数的单调区间.(Ⅱ)通过构造函数
的取值,确定函数的单调区间.(Ⅱ)通过构造函数![]() ,把不等式证明问题转化为函数求最值问题,求函数
,把不等式证明问题转化为函数求最值问题,求函数![]() 当
当![]() 时的最大值小于零即可.(Ⅲ)要充分利用(Ⅰ)(Ⅱ)问的结论.
时的最大值小于零即可.(Ⅲ)要充分利用(Ⅰ)(Ⅱ)问的结论.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】下列命题正确的是__________.(写出所有正确命题的序号)
①已知![]() ,“
,“![]() 且
且![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
②已知平面向量![]() ,“
,“![]() 且
且![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
③已知![]() ,“
,“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
④命题![]() :“
:“![]() ,使
,使![]() 且
且![]() ”的否定为
”的否定为![]() :“
:“![]() ,都有
,都有![]() 且
且![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机厂商推出一次智能手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
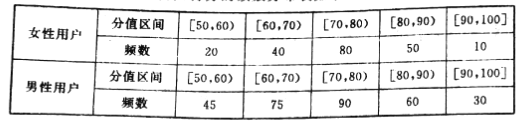
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的方差大小(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取3名用户,求3名用户评分小于90分的人数的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府拟在该地一水库上建造一座水电站,用泄流水量发电.下图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知![]() ,历年中日泄流量在区间[30,60)
,历年中日泄流量在区间[30,60)
的年平均天数为156,一年按364天计.
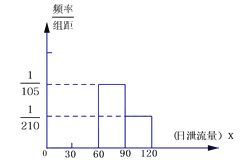
(Ⅰ)请把频率分布直方图补充完整;
(Ⅱ)该水电站希望安装的发电机尽可能运行,但每30万立方米的日泄流量才够运行一台发电机,如![]() 时才够运行两台发电机,若运行一台发电机,每天可获利润为4000元,若不运行,则该台发电机每天亏损500元,以各段的频率作为相应段的概率,以水电站日利润的期望值为决策依据,问:为使水电站日利润的期望值最大,该水电站应安装多少台发电机?
时才够运行两台发电机,若运行一台发电机,每天可获利润为4000元,若不运行,则该台发电机每天亏损500元,以各段的频率作为相应段的概率,以水电站日利润的期望值为决策依据,问:为使水电站日利润的期望值最大,该水电站应安装多少台发电机?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】环境监测中心监测我市空气质量,每天都要记录空气质量指数(指数采取10分制,保留一位小数),现随机抽取20天的指数(见下表),将指数不低于![]() 视为当天空气质量优良.
视为当天空气质量优良.
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
空气质量指数 |
|
|
|
|
|
|
|
|
|
|
天数 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
空气质量指数 |
|
|
|
|
|
|
|
|
|
|
(1)求从这20天随机抽取3天,至少有2天空气质量为优良的概率;
(2)以这20天的数据估计我市总体空气质量(天数很多),若从我市总体空气质量指数中随机抽取3天的指数,用![]() 表示抽到空气质量为优良的天数,求
表示抽到空气质量为优良的天数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com