
甲,乙,丙三位学生独立地解同一道题,甲做对的概率为 ,乙,丙做对的概率分别为
,乙,丙做对的概率分别为 ,
, (
( >
> ),且三位学生是否做对相互独立.记
),且三位学生是否做对相互独立.记 为这三位学生中做对该题的人数,其分布列为:
为这三位学生中做对该题的人数,其分布列为:
 | 0 | 1 | 2 | 3 |
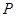 |  | 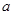 |  |  |
 ,
, 的值;
的值; 的数学期望.
的数学期望.  阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
用分层抽样方法从高中三个年级的相关人员中抽取若干人组成研究小组,有关数据见下表:(单位:人)
(Ⅰ)求 ,
,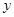 ;
;
(Ⅱ)若从高二、高三年级抽取的人中选 人,求这2人都来自高二年级的概率.
人,求这2人都来自高二年级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个. 求:
(Ⅰ)连续取两次都是红球的概率;
(Ⅱ)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,取球次数最多不超过4次,求取球次数 的概率分布列及期望.
的概率分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
其市有小型超市72个,中型超市24个,大型超市12个,现采用分层抽样方法抽取9个超市对其销售商品质量进行调查.
(I)求应从小型、中型、大型超市分别抽取的个数;
(II)若从抽取的9个超市中随机抽取3个做进一步跟踪分析,记随机变量X为抽取的小型超市的个数,求随机变量X的分布列及数学期望E(X) .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为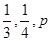 ,
,
且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为 .
.
(1)求 的值,
的值,
(2)设在甲、乙、丙三人中破译出密码的总人数为X,求X的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学作为蓝色海洋教育特色学校,随机抽取100名学生,进行一次海洋知识测试,按测试成绩分组如下:第一组[65,70),第二组 [70,75),第三组[75,80),第四组 [80,85),第五组 [85,90)(假设考试成绩均在[65,90)内),得到频率分布直方图如图:
(1)求测试成绩在[80,85)内的频率;
(2)从第三、四、五组同学中用分层抽样的方法抽取6名同学组成海洋知识宣讲小组,定期在校内进行义务宣讲,并在这6名同学中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,求第四组至少有一名同学被抽中的的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
| 高校 | 相关人数 | 抽取人数 |
| A | 18 |  |
| B | 36 | 2 |
| C | 54 | 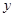 |
 ,
,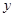 ;
;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了调查某大学学生在周日上网的时间,随机对1OO名男生和100名女生进行了不记 名的问卷调查.得到了如下的统计结果:
表1:男生上网时间与频数分布表
表2:女生上网时间与频数分布表
(I)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数;
(II)完成下面的2x2列联表,并回答能否有90%的把握认为“学生周日上网时间与性 别有关”?
表3: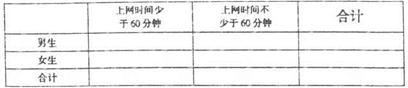

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com