
在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC,AB=2EF.若M是线段AD的中点,
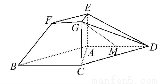
求证:GM∥平面ABFE.
见解析
【解析】证明:方法一:因为EF∥AB,FG∥BC,EG∥AC,∠ACB=90°,

所以∠EGF=90°,
△ABC∽△EFG.
由于AB=2EF,因此BC=2FG.
连接AF,由于FG∥BC,FG=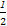 BC,
BC,
在?ABCD中,M是线段AD的中点,则AM∥BC,
且AM=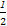 BC,因此FG∥AM且FG=AM,
BC,因此FG∥AM且FG=AM,
所以四边形AFGM为平行四边形,因此GM∥FA.
又FA?平面ABFE,GM?平面ABFE,
所以GM∥平面ABFE.
方法二:因为EF∥AB,FG∥BC,EG∥AC,∠ACB=90°,

∴∠EGF=90°,
△ABC∽△EFG.
由于AB=2EF,∴BC=2FG.
取BC的中点N,连接GN,
因此四边形BNGF为平行四边形,所以GN∥FB.
在?ABCD中,M是线段AD的中点,连接MN,
则MN∥AB.
∵MN∩GN=N,∴平面GMN∥平面ABFE.
又GM?平面GMN,∴GM∥平面ABFE.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(七)第二章第四节练习卷(解析版) 题型:选择题
若函数f(x)=(a+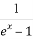 )cosx是奇函数,则常数a的值等于( )
)cosx是奇函数,则常数a的值等于( )
(A)-1 (B)1 (C)- (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷(解析版) 题型:选择题
a,b,c是三条直线,α,β是两个平面,b?α,c?α,则下列命题不成立的是( )
(A)若α∥β,c⊥α,则c⊥β
(B)“若b⊥β,则α⊥β”的逆命题
(C)若a是c在α内的射影,a⊥b,则b⊥c
(D)“若b∥c,则c∥α”的逆否命题
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷(解析版) 题型:填空题
已知a=(1,1,1),b=(0,2,-1),c=ma+nb+(4,-4,1).若c与a及b都垂直,则m,n的值分别为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷(解析版) 题型:选择题
若平面α,β垂直,则下面可以是这两个平面的法向量的是( )
(A)n1=(1,2,1),n2=(-3,1,1)
(B)n1=(1,1,2),n2=(-2,1,1)
(C)n1=(1,1,1),n2=(-1,2,1)
(D)n1=(1,2,1),n2=(0,-2,-2)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十五第七章第四节练习卷(解析版) 题型:选择题
若α,β是两个相交平面,点A不在α内,也不在β内,则过点A且与α和β都平行的直线( )
(A)只有1条 (B)只有2条
(C)只有4条 (D)有无数条
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十二第七章第一节练习卷(解析版) 题型:解答题
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝.再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面).
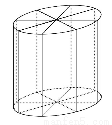
(1)当圆柱底面半径r取何值时,S取得最大值?并求出该最大值(结果精确到0.01平方米).
(2)若要制作一个如图放置的、底面半径为0.3米的灯笼,请作出灯笼的三视图(作图时,不需考虑骨架等因素).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十九第七章第八节练习卷(解析版) 题型:解答题
如图,在四棱锥S-ABCD中,SD⊥底面ABCD,底面ABCD是矩形,SD=AD=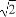 AB,E是SA的中点.
AB,E是SA的中点.

(1)求证:平面BED⊥平面SAB.
(2)求直线SA与平面BED所成角的大小.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十七第七章第六节练习卷(解析版) 题型:选择题
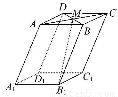
如图,在底面为平行四边形的四棱柱ABCD - A1B1C1D1中,M是AC与BD的交点,若 =a,
=a,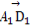 =b,
=b,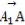 =c,则下列向量中与
=c,则下列向量中与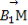 相等的向量是( )
相等的向量是( )
(A)- a+
a+ b+c (B)
b+c (B) a+
a+ b+c (C)
b+c (C) a-
a- b+c (D)-
b+c (D)- a-
a- b+c
b+c
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com