
【题目】已知圆![]() :
:![]() ,其圆心
,其圆心![]() 在抛物线
在抛物线![]() :
:![]() 上,圆
上,圆![]() 过原点且与抛物线
过原点且与抛物线![]() 的准线相切.
的准线相切.
(1)求抛物线![]() 的方程;
的方程;
(2)若过抛物线![]() 的焦点
的焦点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 且垂直于直线
且垂直于直线![]() 的直线交抛物线
的直线交抛物线![]() 的准线于点
的准线于点![]() .求
.求![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 点在
点在![]() 点左边)与直线
点左边)与直线![]() 交于点
交于点![]() .求
.求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)[选修4-5:不等式选讲]
已知函数![]() =|x-a|+
=|x-a|+![]() (a≠0)
(a≠0)
(1)若不等式![]() -
-![]() ≤1恒成立,求实数m的最大值;
≤1恒成立,求实数m的最大值;
(2)当a<![]() 时,函数g(x)=
时,函数g(x)=![]() +|2x-1|有零点,求实数a的取值范围
+|2x-1|有零点,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2015年以来,“一带一路”建设成果显著.如图是2015—2019年,我国对“一带一路”沿线国家进出口情况统计图,下列描述错误的是( )
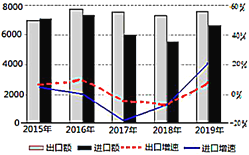
A.这五年,出口总额之和比进口总额之和大
B.这五年,2015年出口额最少
C.这五年,2019年进口增速最快
D.这五年,出口增速前四年逐年下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 相交所得的线段长为3,椭圆的左、右焦点分别为
相交所得的线段长为3,椭圆的左、右焦点分别为![]() ,
,![]() ,动点
,动点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,过
,过![]() ,
,![]() 分别作直线
分别作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() .若
.若![]() ,
,![]() ,
,![]() 的面积成等差数列,求直线
的面积成等差数列,求直线![]() 斜率的取值范围.
斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,直线l1的参数方程为![]() (t为参数),直线l2的参数方程为
(t为参数),直线l2的参数方程为 .设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
.设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ) ![]() =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com