
ЎѕМвДїЎїДіёЯРЈЙијЖБЛТ»ёцКµСйС§їЖµДКµСйїјІй·Ѕ°ёЈєїјЙъґУ6µА±ёСЎМвЦРТ»ґОРФЛж»ъійИЎ3МвЈ¬°ґХХМвДїТЄЗу¶АБўНкіЙИ«ІїКµСйІЩЧчЈ®№ж¶ЁЈєЦБЙЩХэИ·НкіЙЖдЦР2МвµД±гїЙМбЅ»НЁ№эЈ®ТСЦЄ6µА±ёСЎМвЦРїјЙъјЧУР4µАМвДЬХэИ·НкіЙЈ¬2µАМвІ»ДЬНкіЙЈ®
ЈЁ1Ј©ЗуіцјЧїјЙъХэИ·НкіЙМвКэµДёЕВК·ЦІјБРЈ¬ІўјЖЛгКэС§ЖЪНыЈ»
ЈЁ2Ј©ИфїјЙъТТГїМвХэИ·НкіЙµДёЕВК¶јКЗ![]() Ј¬ЗТГїМвХэИ·НкіЙУл·с»ҐІ»У°ПмЈ®КФґУЦБЙЩХэИ·НкіЙ2МвµДёЕВК·ЦОц±ИЅПБЅО»їјЙъµДКµСйІЩЧчДЬБ¦Ј®
Ј¬ЗТГїМвХэИ·НкіЙУл·с»ҐІ»У°ПмЈ®КФґУЦБЙЩХэИ·НкіЙ2МвµДёЕВК·ЦОц±ИЅПБЅО»їјЙъµДКµСйІЩЧчДЬБ¦Ј®
Ўѕґр°ёЎїЈЁ1Ј©јыЅвОцЈ¬2Ј®ЈЁ2Ј©ґЛјЧµДКµСйІЩЧчДЬБ¦ЅПЗїЈ®
ЎѕЅвОцЎї
ЈЁ1Ј©ЙиїјЙъјЧХэИ·НкіЙКµСйІЩЧчµДМвКэ·Ц±рОЄXЈ¬Фт ![]() Ј¬kЈЅ1Ј¬2Ј¬3Ј¬УЙґЛЗуµГїјЙъјЧХэИ·НкіЙКµСйІЩЧчµДМвКэµДёЕВК·ЦІјБРЈ®
Ј¬kЈЅ1Ј¬2Ј¬3Ј¬УЙґЛЗуµГїјЙъјЧХэИ·НкіЙКµСйІЩЧчµДМвКэµДёЕВК·ЦІјБРЈ®
ЈЁ2Ј©ЙиїјЙъТТХэИ·НкіЙКµСйІЩЧчµДМвКэОЄYЈ¬Фт![]() Ј¬ЗуµГPЈЁYЎЭ2Ј©µДЦµЎўPЈЁXЎЭ2Ј©µДЦµЈ¬ФЩёщѕЭPЈЁXЎЭ2Ј©ЈѕPЈЁYЎЭ2Ј©Ј¬µГіцЅбВЫЈ®
Ј¬ЗуµГPЈЁYЎЭ2Ј©µДЦµЎўPЈЁXЎЭ2Ј©µДЦµЈ¬ФЩёщѕЭPЈЁXЎЭ2Ј©ЈѕPЈЁYЎЭ2Ј©Ј¬µГіцЅбВЫЈ®
ЈЁ1Ј©ЙиїјЙъјЧХэИ·НкіЙКµСйІЩЧчµДМвКэ·Ц±рОЄXЈ¬
Фт ![]() Ј¬kЈЅ1Ј¬2Ј¬3Ј®
Ј¬kЈЅ1Ј¬2Ј¬3Ј®
ЛщТФїјЙъјЧХэИ·НкіЙКµСйІЩЧчµДМвКэµДёЕВК·ЦІјБРОЄЈє
X | 1 | 2 | 3 |
P |
|
|
|
ЎаEXЈЅ1![]() 2
2![]() 3
3![]() 2Ј®
2Ј®
ЈЁ2Ј©ЙиїјЙъТТХэИ·НкіЙКµСйІЩЧчµДМвКэОЄYЈ¬Фт![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() Ј¬kЈЅ0Ј¬1Ј¬2Ј¬3Ј¬
Ј¬kЈЅ0Ј¬1Ј¬2Ј¬3Ј¬
![]() Ј»
Ј»
УЦ![]() Ј¬ЗТPЈЁXЎЭ2Ј©ЈѕPЈЁYЎЭ2Ј©Ј¬
Ј¬ЗТPЈЁXЎЭ2Ј©ЈѕPЈЁYЎЭ2Ј©Ј¬
ґУЦБЙЩХэИ·НкіЙ2МвµДёЕВКїјІмЈ¬јЧНЁ№эµДїЙДЬРФґуЈ¬ТтґЛјЧµДКµСйІЩЧчДЬБ¦ЅПЗїЈ®


 ФД¶БїміµПµБРґр°ё
ФД¶БїміµПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() .
.
ЈЁ1Ј©Иф![]() .Ц¤ГчєЇКэ
.Ц¤ГчєЇКэ![]() УРЗТЅцУРБЅёцБгµгЈ»
УРЗТЅцУРБЅёцБгµгЈ»
ЈЁ2Ј©ИфєЇКэ![]() ґжФЪБЅёцБгµг
ґжФЪБЅёцБгµг![]() Ј¬Ц¤ГчЈє
Ј¬Ц¤ГчЈє![]() .
.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄХэ·ЅМе![]() µДАві¤ОЄ
µДАві¤ОЄ![]() ОЄ
ОЄ![]() µДЦРµгЈ¬ПВБРЛµ·ЁЦРХэИ·µДКЗЈЁ Ј©
µДЦРµгЈ¬ПВБРЛµ·ЁЦРХэИ·µДКЗЈЁ Ј©
A.![]() Ул
Ул![]() ЛщіЙµДЅЗґуУЪ
ЛщіЙµДЅЗґуУЪ![]()
B.µг![]() µЅЖЅГж
µЅЖЅГж![]() µДѕаАлОЄ1
µДѕаАлОЄ1
C.ИэАвЧ¶![]() µДНвЅУЗтµД±нГж»эОЄ
µДНвЅУЗтµД±нГж»эОЄ![]()
D.Ц±ПЯ![]() УлЖЅГж
УлЖЅГж![]() ЛщіЙµДЅЗОЄ
ЛщіЙµДЅЗОЄ![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬ЗъПЯCµДІОКэ·ЅіМОЄ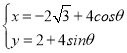 ЈЁ¦ИОЄІОКэЈ©Ј¬Ц±ПЯlµДІОКэ·ЅіМОЄ
ЈЁ¦ИОЄІОКэЈ©Ј¬Ц±ПЯlµДІОКэ·ЅіМОЄ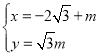 ЈЁmОЄІОКэЈ©Ј¬ТФЖЅГжЦ±ЅЗЧш±кПµµДФµгOОЄј«µгЈ¬xЦбХэ°лЦбОЄј«ЦбЈ¬ЅЁБўЧш±кПµЈ®
ЈЁmОЄІОКэЈ©Ј¬ТФЖЅГжЦ±ЅЗЧш±кПµµДФµгOОЄј«µгЈ¬xЦбХэ°лЦбОЄј«ЦбЈ¬ЅЁБўЧш±кПµЈ®
ЈЁ1Ј©ЗуЗъПЯCµДј«Чш±к·ЅіМЈ»
ЈЁ2Ј©Ц±ПЯlУлЗъПЯCПаЅ»УЪMЈ¬NБЅµгЈ¬Иф![]() Ј¬Зу
Ј¬Зу![]() µДЦµЈ®
µДЦµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ЛДАвЧ¶A©ЃBCDEЦРЈ¬ABЎўBCЎўBEБЅБЅґ№Ц±ЗТABЈЅBCЈЅBEЈ¬DEЎОBCЈ¬DEЈЅ2BCЈ¬FКЗAEµДЦРµгЈ®
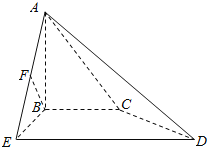
ЈЁ1Ј©ЗуЦ¤ЈєBFЎОГжACDЈ»
ЈЁ2Ј©ЗуЦ¤ЈєГжADEЎНГжACDЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјўЩЈєФЪЖЅРРЛД±ЯРО![]() ЦР,
ЦР,![]() ,
,![]() ,Ѕ«
,Ѕ«![]() СШ¶ФЅЗПЯ
СШ¶ФЅЗПЯ![]() ХЫЖр,К№
ХЫЖр,К№![]() ,Б¬Ѕб
,Б¬Ѕб![]() ,µГµЅИзНјўЪЛщКѕИэАвЧ¶
,µГµЅИзНјўЪЛщКѕИэАвЧ¶![]() .
.
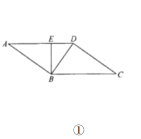
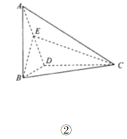
ЈЁ1Ј©Ц¤ГчЈє![]() ЖЅГж
ЖЅГж![]() Ј»
Ј»
ЈЁ2Ј©Иф![]() ,¶юГжЅЗ
,¶юГжЅЗ![]() µДЖЅГжЅЗµДХэЗРЦµОЄ
µДЖЅГжЅЗµДХэЗРЦµОЄ![]() ,ЗуЦ±ПЯ
,ЗуЦ±ПЯ![]() УлЖЅГж
УлЖЅГж![]() ЛщіЙЅЗµДХэПТЦµ.
ЛщіЙЅЗµДХэПТЦµ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЛДАвЧ¶![]() ЦРЈ¬µЧГж
ЦРЈ¬µЧГж![]() КЗЖЅРРЛД±ЯРОЈ¬
КЗЖЅРРЛД±ЯРОЈ¬![]() Ј¬ЖЅГж
Ј¬ЖЅГж![]() µЧГж
µЧГж![]() Ј¬ЗТ
Ј¬ЗТ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ·Ц±рОЄ
·Ц±рОЄ![]() Ј¬
Ј¬![]() µДЦРµг.
µДЦРµг.
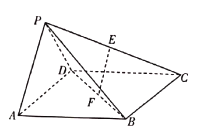
ЈЁ1Ј©ЗуЦ¤Јє![]() ЖЅГж
ЖЅГж![]() Ј»
Ј»
ЈЁ2Ј©ЗуЦ¤ЈєЖЅГж![]() ЖЅГж
ЖЅГж![]() Ј»
Ј»
ЈЁ3Ј©ЗуИэАвЧ¶![]() µДМе»э.
µДМе»э.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїПВБР№ШУЪєЇКэ![]() µДРрКцХэИ·µДОЄ( )
µДРрКцХэИ·µДОЄ( )
A.єЇКэ![]() УРИэёцБгµг
УРИэёцБгµг
B.µг(1Ј¬0)КЗєЇКэ![]() НјПуµД¶ФіЖЦРРД
НјПуµД¶ФіЖЦРРД
C.єЇКэ![]() µДј«ґуЦµµгОЄ
µДј«ґуЦµµгОЄ![]()
D.ґжФЪКµКэaЈ¬К№µГєЇКэ![]() ОЄФцєЇКэ
ОЄФцєЇКэ
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() ФЪ
ФЪ![]() ЙПµДЧоґуЦµОЄ
ЙПµДЧоґуЦµОЄ![]() .
.
ЈЁ1Ј©Зу![]() µДЅвОцКЅЈ»
µДЅвОцКЅЈ»
ЈЁ2Ј©МЦВЫ![]() µДБгµгµДёцКэ.
µДБгµгµДёцКэ.
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com