
分析 ( I)对于不等式|x+1|+|x-5|≥10,分类讨论求得它的解集.
(Ⅱ)利用绝对值三角不等式求得f(x)的最小值为6,可得6≥$\frac{4}{t}$+2,由此求得t的范围.
解答 解:( I)对于不等式|x+1|+|x-5|≥10,
①当x≤-1时,-2x+4≥10,∴x≤-3,∴x≤-3;
②当-1<x≤5时,6≥10,不成立.
③当x>5时,2x-4≥10,∴x≥7,∴x≥7.
综上可知:不等式的解集为 (-∞,-3]∪[7,+∞).
( II)∵f(x)=|x+1|+|x-5|≥|x+1-x+5|=6,f(x)≥$\frac{4}{t}$+2对任意的实数x恒成立,
∴$\frac{4}{t}+2≤6$,
∴$\frac{1}{t}≤1$,
∴t∈(-∞,0)∪[1,+∞).
点评 本题主要考查绝对值三角不等式,绝对值不等式的解法,体现了等价转化和分类讨论的数学思想,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
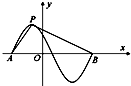 函数f(x)=cos(πx+φ)(φ>0)的图象如图所示,设P是图象的最高点,A、B是图象与x轴的交点,则tan∠APB=( )
函数f(x)=cos(πx+φ)(φ>0)的图象如图所示,设P是图象的最高点,A、B是图象与x轴的交点,则tan∠APB=( )| A. | 10 | B. | 8 | C. | $\frac{8}{7}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面.
如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{12}$个单位 | ||
| C. | 向右平移$\frac{π}{6}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | a<b<c | C. | a>b>c | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校从参加2015年高考的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到部分频率分布直方图(如图所示).观察图中数据,回答下列问题.
某校从参加2015年高考的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到部分频率分布直方图(如图所示).观察图中数据,回答下列问题.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>ab>ab2 | B. | ab2>ab>a | C. | ab>a>ab2 | D. | ab>ab2>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,∠ACB=90°,2AC=AA1,D,M分别是棱AA1,BC的中点.证明:
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,∠ACB=90°,2AC=AA1,D,M分别是棱AA1,BC的中点.证明:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com