
【题目】已知函数![]() .
.
(1)若函数![]() 有极值,求实数
有极值,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,若
时,若![]() 在
在![]() ,
,![]() 处导数相等,证明:
处导数相等,证明:![]() ;
;
(3)若函数![]() 在
在![]() 上有两个零点
上有两个零点![]() ,
,![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)证明见解析;(3)证明见解析
;(2)证明见解析;(3)证明见解析
【解析】
(1)对函数求导,根据导函数存在穿过型零点求解;
(2)由![]() 得出
得出![]() ,利用基本不等式得出
,利用基本不等式得出![]() ,然后计算
,然后计算![]() 可得证;
可得证;
(3)![]() 转化为
转化为![]() ,通过研究
,通过研究![]() 的单调性、极值得出
的单调性、极值得出![]() 的两个零点的范围,不妨设不妨设
的两个零点的范围,不妨设不妨设![]() ,然后分类讨论,若
,然后分类讨论,若![]() ,则结论成立;
,则结论成立;
若![]() ,即
,即![]() 时,构造新函数
时,构造新函数![]() ,
,![]() ,通过导数(需两次求导)得出
,通过导数(需两次求导)得出![]() 的单调性,由
的单调性,由![]() 的关系:
的关系:![]() .可证得结论,
.可证得结论,
解:(1)由题意知![]() ,
,
因为![]() 有极值,所以当
有极值,所以当![]() ,
,![]() 有解,所以
有解,所以![]() .
.
(2)证明:![]() ,由
,由![]() ,
,
得![]() ,
,
即![]() ,
,
因为![]() ,且
,且![]() ,
,
所以![]() ,得
,得![]() ,
,
则![]() .
.
(3)证明:![]() ,
,
即![]() ,令
,令![]() ,则
,则![]() ,
,
则函数![]() 在
在![]() 上单调递减,
上单调递减,
在![]() 上单调递增,
上单调递增,![]() .
.
令![]() ,其中
,其中![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() ,
,
从而当![]() 时有两个零点,
时有两个零点,
不妨设![]() ,
,
若![]() ,则结论成立;
,则结论成立;
若![]() ,即
,即![]() 时,
时,
令![]() ,
,![]() ,
,
则![]() ,
,
令![]() ,则
,则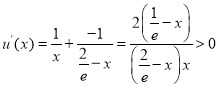 ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
则![]() ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,
,
即![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() ,
,
∵![]() ,
,![]() ,
,
而![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,即
,即![]() .
.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】我国南北朝时期的数学家祖暅提出了计算几何体体积的祖暅原理:“幂势既同,则积不容异“.意思是两个同高的几何体,如果在等高处的截面积都相等,那么这两个几何体的体积相等.现有某几何体和一个圆锥满足祖暅原理的条件,若该圆锥的侧面展开图是半径为3的圆的三分之一,则该几何体的体积为( )
A.![]() πB.
πB.![]() πC.4
πC.4![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是2020项的实数数列,
是2020项的实数数列,![]() 中的每一项都不为零,
中的每一项都不为零,![]() 中任意连续11项
中任意连续11项![]() 的乘积是定值
的乘积是定值![]() .
.
①存在满足条件的数列,使得其中恰有365个1;
②不存在满足条件的数列,使得其中恰有550个1.
命题的真假情况为( )
A.①和②都是真命题B.①是真命题,②是假命题
C.②是真命题,①是假命题D.①和②都是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率为
的离心率为![]() ,左焦点
,左焦点![]() 到直线
到直线![]() 的距离为10,圆
的距离为10,圆![]() .
.
(1)求椭圆的方程;
(2)若![]() 是椭圆上任意一点,
是椭圆上任意一点,![]() 为圆
为圆![]() 的任一直径,求
的任一直径,求![]() 的取值范围;
的取值范围;
(3)是否存在以椭圆上点![]() 为圆心的圆
为圆心的圆![]() ,使得过圆
,使得过圆![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线,切点为
的切线,切点为![]() ,都满足
,都满足![]() ?若存在,求出圆
?若存在,求出圆![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() .以
.以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,连接
,连接![]() 和
和![]() .
.
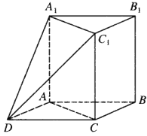
(1)求证:![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 与平面
与平面![]() 垂直?若存在,求出
垂直?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
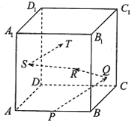
【题目】如图,在正方体![]() 中,棱
中,棱![]() 的中点为
的中点为![]() ,若光线从点
,若光线从点![]() 出发,依次经三个侧面
出发,依次经三个侧面![]() ,
,![]() ,
,![]() 反射后,落到侧面
反射后,落到侧面![]() (不包括边界),则入射光线
(不包括边界),则入射光线![]() 与侧面
与侧面![]() 所成角的正切值的范围是( )
所成角的正切值的范围是( )
A.![]() B.
B.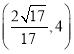 C.
C. D.
D.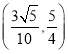
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“勾股定理”在西方被称为“毕达哥拉斯定理”,国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明![]() 如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形
如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形![]() 若直角三角形中较小的锐角
若直角三角形中较小的锐角![]() ,现在向该大止方形区域内随机地投掷一枚飞镖,则飞镖落在阴影部分的概率是
,现在向该大止方形区域内随机地投掷一枚飞镖,则飞镖落在阴影部分的概率是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车又称为小黄车,近年来逐渐走进了人们的生活,也成为减少空气污染,缓解城市交通压力的一种重要手段.为调查某地区居民对共享单车的使用情况,从该地区居民中按年龄用随机抽样的方式随机抽取了![]() 人进行问卷调查,得到这
人进行问卷调查,得到这![]() 人对共享单车的评价得分统计填入茎叶图,如下所示(满分
人对共享单车的评价得分统计填入茎叶图,如下所示(满分![]() 分):
分):

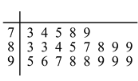
(1)找出居民问卷得分的众数和中位数;
(2)请计算这![]() 位居民问卷的平均得分;
位居民问卷的平均得分;
(3)若在成绩为![]() 分的居民中随机抽取
分的居民中随机抽取![]() 人,求恰有
人,求恰有![]() 人成绩超过
人成绩超过![]() 分的概率.
分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com