
如图,椭圆![]() 的一个焦点是F(1,0),O为坐标原点.
的一个焦点是F(1,0),O为坐标原点.
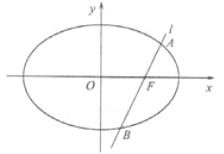
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(Ⅱ)设过点F的直线l交椭圆于A、B两点.若直线l绕点F任意转动,恒有
![]() ,求a的取值范围.
,求a的取值范围.
解法一:(Ⅰ)设M,N为短轴的两个三等分点,因为△MNF为正三角形,

所以![]() ,即1=
,即1=![]() ,解得
,解得![]()
![]() 因此,椭圆方程为
因此,椭圆方程为![]()
(Ⅱ)设![]()
()当直线 AB与x轴重合时,

()当直线AB不与x轴重合时,
设直线AB的方程为:![]()
整理得![]()
所以![]()
因为恒有![]() ,所以
,所以![]() AOB恒为钝角.
AOB恒为钝角.
即![]() 恒成立.
恒成立.
![]()

又a2+b2m2>0,所以-m2a2b2+b2-a2b2+a2<0对m![]() R恒成立,
R恒成立,
即a2b2m2> a2 -a2b2+b2对m![]() R恒成立.
R恒成立.
当m![]() R时,a2b2m2最小值为0,所以a2- a2b2+b2<0.
R时,a2b2m2最小值为0,所以a2- a2b2+b2<0.
a2<a2b2- b2, a2<( a2-1)b2= b4,
因为a>0,b>0,所以a<b2,即a2-a-1>0,
解得a>![]() 或a<
或a<![]() (舍去),即a>
(舍去),即a>![]() ,
,
综合(i)(ii),a的取值范围为(![]() ,+
,+![]() ).
).
解法二:
(Ⅰ)同解法一,
(Ⅱ)解:(i)当直线l垂直于x轴时,
x=1代入![]()
因为恒有|OA|2+|OB|2<|AB|2,2(1+yA2)<4 yA2, yA2>1,即![]() >1,
>1,
解得a>![]() 或a<
或a<![]() (舍去),即a>
(舍去),即a>![]() .
.
(ii)当直线l不垂直于x轴时,设A(x1,,y1), B(x2,y2).
设直线AB的方程为y=k(x-1)代入![]()
得(b2+a2k2)x2-2a2k2x+ a2 k2- a2 b2=0,
故x1+x2=![]()
因为恒有|OA|2+|OB|2<|AB|2,
所以x21+y21+ x22+ y22<( x2-x1)2+(y2-y1)2,得x1x2+ y1y2<0恒成立.
x1x2+ y1y2= x1x2+k2(x1-1) (x2-1)=(1+k2) x1x2-k2(x1+x2)+ k2
=(1+k2)![]() .
.
由题意得(a2- a2 b2+b2)k2- a2 b2<0对k![]() R恒成立.
R恒成立.
①当a2- a2 b2+b2>0时,不合题意;
②当a2- a2 b2+b2=0时,a=![]() ;
;
③当a2- a2 b2+b2<0时,a2- a2(a2-1)+ (a2-1)<0,a4- 3a2 +1>0,
解得a2>![]() 或a2>
或a2>![]() (舍去),a>
(舍去),a>![]() ,因此a
,因此a![]()
![]() .
.
综合(i)(ii),a的取值范围为(![]() ,+
,+![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(08年福建卷理)(本小题满分12分)
如图,椭圆![]() 的一个焦点是
的一个焦点是![]() ,O为坐标原点.
,O为坐标原点.
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角
形,求椭圆的方程;
(Ⅱ)设过点F的直线l交椭圆于A、B两点.若直线l绕点F
任意转动,恒有![]() ,求a的取值范围.
,求a的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
(08年福建卷理)(本小题满分12分)
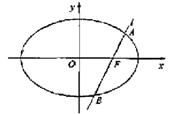
如图,椭圆![]() 的一个焦点是
的一个焦点是![]() ,O为坐标原点.
,O为坐标原点.
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角
形,求椭圆的方程;
(Ⅱ)设过点F的直线l交椭圆于A、B两点.若直线l绕点F
任意转动,恒有![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年福建卷文)(本小题满分14分)
如图,椭圆![]() 的一个焦点是
的一个焦点是![]() ,且过点
,且过点![]() 。
。
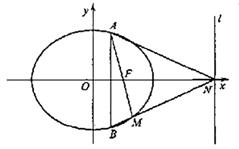
(Ⅰ)求椭圆C的方程;
(Ⅱ)若AB为垂直于x轴的动弦,直线![]() 与x轴交于点N,直线AF与BN交于点M。
与x轴交于点N,直线AF与BN交于点M。
()求证:点M恒在椭圆C上;
()求![]() 面积的最大值。
面积的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
如图,椭圆![]() 的一个焦点是F(1,0),O为坐标原点。
的一个焦点是F(1,0),O为坐标原点。

(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(Ⅱ)设过点F的直线l交椭圆于A、B两点,若直线l绕点F任意转动,值有![]() ,求a的取值范围。
,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校招生全国统一考试理科数学(福建卷) 题型:选择题
(本小题满分12分)
如图,椭圆 的一个焦点是F(1,0),O为坐标原点。
的一个焦点是F(1,0),O为坐标原点。
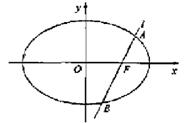
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(Ⅱ)设过点F的直线l交椭圆于A、B两点,若直线l绕点F任意转动,值有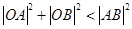 ,求a的取值范围。
,求a的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com