
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间和极值;
的单调区间和极值;
(2)若![]() 恒成立;求实数
恒成立;求实数![]() 的值.
的值.
【答案】(1)函数![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() ,极小值为
,极小值为![]() ,无极大值;(2)
,无极大值;(2)![]() .
.
【解析】
试题分析:(1)求出导数![]() 及定义域,在定义域内解不等式
及定义域,在定义域内解不等式![]() 得增区间,解不等式
得增区间,解不等式![]() 得减区间,同时可确定极值;(2)设
得减区间,同时可确定极值;(2)设![]() ,求出导数
,求出导数![]() ,研究
,研究![]() 的单调性,不等式
的单调性,不等式![]() 恒成立,即
恒成立,即![]() 的最小值非负,因此由导数求得
的最小值非负,因此由导数求得![]() 的最小值,由于
的最小值,由于![]() ,因此当
,因此当![]() 时,
时,![]() 单调递增,不合题意(
单调递增,不合题意(![]() ),
),![]() 时,
时,![]() ,再由函数
,再由函数![]() 的单调性可得只有
的单调性可得只有![]() 时,
时,![]()
![]() ,从而确定
,从而确定![]() .
.
试题解析:(1)注意到函数![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时,![]() ,若
,若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() .
.
所以![]() 是
是![]() 上的减函数,是
上的减函数,是![]() 上的增函数,故
上的增函数,故![]() ,故函数
,故函数![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() ,极小值为
,极小值为![]() ,无极大值.
,无极大值.
(2)由(1)知![]() ,当
,当![]() 时,
时,![]() 时,
时,![]() 是
是![]() 上的增函数,注意到
上的增函数,注意到![]() 时,
时,![]() ,不合题意.当
,不合题意.当![]() 时,若
时,若![]() ;若
;若![]() .所以
.所以![]() 是
是![]() 上的减函数,是
上的减函数,是![]() 上的增函数,故只需
上的增函数,故只需![]() .令
.令![]() ,当
,当![]() 时,
时,
![]() ;当
;当![]() 时,
时,![]() .所以
.所以![]() 是
是![]() 上的减函数,是
上的减函数,是![]() 上的增函数.
上的增函数.
故![]() 当且仅当
当且仅当![]() 时等号成立. 即
时等号成立. 即![]() 所求.
所求.


科目:高中数学 来源: 题型:
【题目】某单位员工![]() 人参加“学雷锋”志愿活动,按年龄分组:第组
人参加“学雷锋”志愿活动,按年龄分组:第组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)下表是年龄的频率分布表,求正整数![]() 的值;
的值;
区间 |
|
|
|
|
|
人数 |
|
|
|
|
|
(2)现在要从年龄较小的第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,年龄在第
人,年龄在第![]() 组抽取的员工的人数分别是多少?
组抽取的员工的人数分别是多少?
(3)在(2)的前提下,从这![]() 人中随机抽取
人中随机抽取![]() 人参加社区宣传交流活动,求至少有人年龄在第
人参加社区宣传交流活动,求至少有人年龄在第![]() 组的概率.
组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是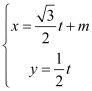 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中是公理的是
A. 在空间中,如果两个角的两条边对应平行,那么这两个角相等或互补
B. 如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直
C. 平行于同一条直线的两条直线平行
D. 如果两个平行平面同时与第三个平面相交,那么它们的交线平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个年级有12个班,每个班有50名学生,按1到50排学号,为了交流学习经验,要求每班学号为14的学生留下进行交流,这里运用的是( )
A. 分层抽样 B. 抽签法
C. 随机数表法 D. 系统抽样
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com