
 为5 000元,而每生产100台产品时直接消耗成本要增加2 500
为5 000元,而每生产100台产品时直接消耗成本要增加2 500 元,市场对此商品年需求量为500台,销售的收入函数为
元,市场对此商品年需求量为500台,销售的收入函数为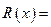
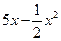 (万元)(0≤
(万元)(0≤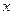 ≤5),其中
≤5),其中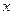 是产品售出的数量(单位:百台)
是产品售出的数量(单位:百台) 多少时,企业所得的利润最大;
多少时,企业所得的利润最大; 0.1 百台或5<x<48 百台,即企业年产量在10台到4 800台之间时,企业不亏本.
0.1 百台或5<x<48 百台,即企业年产量在10台到4 800台之间时,企业不亏本.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 2分)
2分) 验发现,若按每件
验发现,若按每件 20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y(件)是价格x(元/件)的一次函数.
20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y(件)是价格x(元/件)的一次函数. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 件)是价格x(元/件)的
件)是价格x(元/件)的 一次函数.
一次函数. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com