
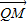 +3
+3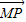 =
= ,
,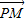 •
• =1.
=1. ,与
,与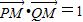 ,再化简,就可得点M的轨迹C的方程.
,再化简,就可得点M的轨迹C的方程.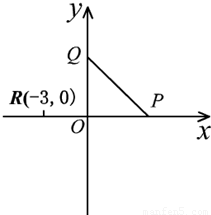 解:(1)设M(x,y),由
解:(1)设M(x,y),由 ,得P(
,得P( ,0),Q(0,-
,0),Q(0,- )
) 得(
得( ,0)•(0,-
,0)•(0,- )=1,
)=1, ,
,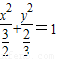 (x>0)
(x>0)
 ,m=±
,m=±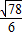 ,
, (x>0)表示椭圆在y轴右边部分.
(x>0)表示椭圆在y轴右边部分.
 的上顶点B(0,
的上顶点B(0, ),
), ≤m<
≤m<
 ,
, ].
].

 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
| PM |
| MQ |
| 0 |
| RP |
| PM |
| AB |
| AN |
| 16 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| QM |
| MP |
| 0 |
| PM |
| QM |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点R(-3,0),点P在![]() 轴的正半轴上,点Q在
轴的正半轴上,点Q在![]() 轴上,点M在直线PQ上,且满足
轴上,点M在直线PQ上,且满足![]() .
.
(1)求点M的轨迹C的方程;
(2)设直线![]() 与曲线C恒有公共点,求
与曲线C恒有公共点,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源:2006-2007学年江苏省扬州市高三(下)调研数学试卷(解析版) 题型:解答题
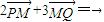 ,
,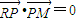 .
.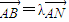 ,且
,且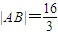 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com