
分析 (1)利用向量的数量积运算、夹角公式即可得出;
(2)利用由$\overrightarrow n⊥\overrightarrow q$确定出$\overrightarrow{n}$,利用三角形的余弦定理求出∠B,利用向量模的坐标公式求出$|\overrightarrow n+\overrightarrow p|$2,利用三角函数的二倍角公式化简三角函数,利用整体思想求出三角函数的取值范围.
解答 解:(1)设$\overrightarrow{n}$=(x,y),由$\overrightarrow{m}•\overrightarrow{n}$=-1,x+y=1,
$\overrightarrow{n}$与向量$\overrightarrow{m}$夹角为$\frac{3}{4}$π,有$\overrightarrow{m}•\overrightarrow{n}$=|$\overline{m}$||$\overrightarrow{n}$|cos$\frac{3π}{4}$=-1,
所以$|\overrightarrow n|=1$,则x2+y2=1.
解得$\left\{\begin{array}{l}x=-1\\ y=0\end{array}\right.$或$\left\{\begin{array}{l}x=0\\ y=-1\end{array}\right.$,即$\overrightarrow n=(-1\;,\;\;0)$或$\overrightarrow n=(0\;,\;\;-1)$.
(2)由$\overrightarrow n⊥\overrightarrow q$垂直知$\overrightarrow n=(0\;,\;\;-1)$,由2B=A+C知$B=\frac{π}{3}\;,\;\;A+C=\frac{2π}{3}$
若$\overrightarrow n=(0\;,\;\;-1)$,则$\overrightarrow n+\overrightarrow p=(cosA\;,\;\;2{cos^2}\frac{C}{2}-1)=(cosA\;,\;\;cosC)$,
$|\overrightarrow n+\overrightarrow p{|^2}={cos^2}A+{cos^2}C=\frac{1+cos2A}{2}+\frac{1+cos2C}{2}$=$1+\frac{1}{2}[cos2A+cos(\frac{4π}{3}-2A)]=1+\frac{1}{2}cos(2A+\frac{π}{3})$,
0<A<$\frac{2π}{3}$,$\frac{π}{3}$<2A+$\frac{π}{3}$<$\frac{5π}{3}$,则$\frac{1}{2}\;≤\;1+\frac{1}{2}cos(2A+\frac{π}{3})<\frac{5}{4}$.
则|$\overrightarrow{n}$+$\overrightarrow{p}$|∈[$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{5}}{2}$).
点评 本题考查了向量的数量积运算性质、夹角公式、倍角公式、和差化积、三角函数的单调性,考查了推理能力与计算能力,属于中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+6 | B. | 6x-2 | C. | 3x-1 | D. | x+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | (-∞,2) | C. | (4,+∞) | D. | [4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
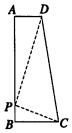 如图所示,在直角梯形ABCD中,AB=7,AD=2,BC=3.如果AB边上的点P使得以P,A,D为顶点的三角形和以P,B,C为顶点的三角形相似,那么这样的点P有( )
如图所示,在直角梯形ABCD中,AB=7,AD=2,BC=3.如果AB边上的点P使得以P,A,D为顶点的三角形和以P,B,C为顶点的三角形相似,那么这样的点P有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com