±¾Ģā°üĄØ£Ø1£©”¢£Ø2£©”¢£Ø3£©”¢£Ø4£©ĖÄŠ”Ģā£¬ĒėŃ”¶ØĘäÖŠĮ½Ģā£¬²¢ŌŚ“šĢāæØÖø¶ØĒųÓņÄŚ“š£¬
Čō¶ą×ö£¬Ōņ°“×÷“šµÄĒ°Į½ĢāĘĄ·Ö£®½ā“šŹ±Ó¦Š“³öĪÄ×ÖĖµĆ÷”¢Ö¤Ć÷¹ż³Ģ»ņŃŻĖć²½Öč£®
£Ø1£©”¢Ń”ŠŽ4-1£ŗ¼øŗĪÖ¤Ć÷Ń”½²
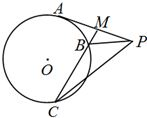
ČēĶ¼£¬”ĻPAQŹĒÖ±½Ē£¬Ō²OÓėAPĻąĒŠÓŚµćT£¬ÓėAQĻą½»ÓŚĮ½µćB£¬C£®ĒóÖ¤£ŗBTĘ½·Ö”ĻOBA
£Ø2£©Ń”ŠŽ4-2£ŗ¾ŲÕóÓė±ä»»£Ø±¾Š”ĢāĀś·Ö10·Ö£©
ČōµćA£Ø2£¬2£©ŌŚ¾ŲÕó

¶ŌÓ¦±ä»»µÄ×÷ÓĆĻĀµĆµ½µÄµćĪŖB£Ø-2£¬2£©£¬Ēó¾ŲÕóMµÄÄę¾ŲÕó
£Ø3£©Ń”ŠŽ4-2£ŗ¾ŲÕóÓė±ä»»£Ø±¾Š”ĢāĀś·Ö10·Ö£©
ŌŚ¼«×ų±źĻµÖŠ£¬AĪŖĒśĻߦŃ
2+2¦Ńcos¦Č-3=0ÉĻµÄ¶Æµć£¬BĪŖÖ±ĻߦŃcos¦Č+¦Ńsin¦Č-7=0ÉĻµÄ¶Æµć£¬ĒóABµÄ×īŠ”Öµ£®
£Ø4£©Ń”ŠŽ4-5£ŗ²»µČŹ½Ń”½²£Ø±¾Š”ĢāĀś·Ö10·Ö£©
ŅŃÖŖa
1£¬a
2”a
n¶¼ŹĒÕżŹż£¬ĒŅa
1•a
2”a
n=1£¬ĒóÖ¤£ŗ£Ø2+a
1£©£Ø2+a
2£©”£Ø2+a
n£©”Ż3
n£®


 ¶ŌÓ¦±ä»»µÄ×÷ÓĆĻĀµĆµ½µÄµćĪŖB£Ø-2£¬2£©£¬Ēó¾ŲÕóMµÄÄę¾ŲÕó
¶ŌÓ¦±ä»»µÄ×÷ÓĆĻĀµĆµ½µÄµćĪŖB£Ø-2£¬2£©£¬Ēó¾ŲÕóMµÄÄę¾ŲÕó
 £¾0£¬¶Ōø÷Ļī·ÅĖõŗó£¬ŌŁĄūÓĆ²»µČŹ½µÄŠŌÖŹĶ¬Ļņ²»µČŹ½Ļą³Ė£®
£¾0£¬¶Ōø÷Ļī·ÅĖõŗó£¬ŌŁĄūÓĆ²»µČŹ½µÄŠŌÖŹĶ¬Ļņ²»µČŹ½Ļą³Ė£®
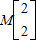 =
= £¬¼“
£¬¼“ =
= £¬
£¬ £¬ÓÉM-1M=
£¬ÓÉM-1M= £¬
£¬ £®
£® =4
=4 £¬ĖłŅŌ|AB|min=4
£¬ĖłŅŌ|AB|min=4 -2£®
-2£® £¾0£»”£Ø2·Ö£©
£¾0£»”£Ø2·Ö£© £¾0£»”£¬2+an=1+1+an”Ż
£¾0£»”£¬2+an=1+1+an”Ż £¾0
£¾0 ”£Ø4·Ö£©
”£Ø4·Ö£©

 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
 Ń”×öĢā±¾Ģā°üĄØA£¬B£¬C£¬DĖÄŠ”Ģā£¬ĒėŃ”¶ØĘäÖŠ Į½Ģā ×÷“š£¬Ć抔Ģā10·Ö£¬¹²¼Ę20·Ö£¬
Ń”×öĢā±¾Ģā°üĄØA£¬B£¬C£¬DĖÄŠ”Ģā£¬ĒėŃ”¶ØĘäÖŠ Į½Ģā ×÷“š£¬Ć抔Ģā10·Ö£¬¹²¼Ę20·Ö£¬ ±¾Ģā°üĄØ£Ø1£©”¢£Ø2£©”¢£Ø3£©”¢£Ø4£©ĖÄŠ”Ģā£¬ĒėŃ”¶ØĘäÖŠĮ½Ģā£¬²¢ŌŚ“šĢāæØÖø¶ØĒųÓņÄŚ“š£¬
±¾Ģā°üĄØ£Ø1£©”¢£Ø2£©”¢£Ø3£©”¢£Ø4£©ĖÄŠ”Ģā£¬ĒėŃ”¶ØĘäÖŠĮ½Ģā£¬²¢ŌŚ“šĢāæØÖø¶ØĒųÓņÄŚ“š£¬ £Ø2012•ŠģÖŻÄ£Äā£©±¾Ģā°üĄØA”¢B”¢C”¢DĖÄŠ”Ģā£¬ĒėŃ”¶ØĘäÖŠĮ½Ģā£¬²¢ŌŚ“šĢāæØÖø¶ØĒųÓņÄŚ×÷“š£¬
£Ø2012•ŠģÖŻÄ£Äā£©±¾Ģā°üĄØA”¢B”¢C”¢DĖÄŠ”Ģā£¬ĒėŃ”¶ØĘäÖŠĮ½Ģā£¬²¢ŌŚ“šĢāæØÖø¶ØĒųÓņÄŚ×÷“š£¬