
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(1)若![]() ,求函数
,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在定义域上恰有两个不同的零点,求实数a的取值范围;
在定义域上恰有两个不同的零点,求实数a的取值范围;
(3)设函数![]() 在区间
在区间![]() )上存在极值,求证:
)上存在极值,求证:![]() .
.
【答案】(1)![]() (2)
(2)![]() 或
或![]() (3)证明见解析
(3)证明见解析
【解析】
(1)利用导数求函数![]() 在
在![]() 处的切线方程;(2)对
处的切线方程;(2)对![]() 分
分![]() 两种情况讨论,当
两种情况讨论,当![]() 时,再分三种情况结合导数分类讨论;(3)先求出
时,再分三种情况结合导数分类讨论;(3)先求出![]() ,要使得
,要使得![]() 在
在![]() 上存在极值,则须满足
上存在极值,则须满足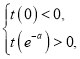 即
即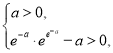 分析推理即可得到
分析推理即可得到![]() .
.
(1)当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以函数![]() 在
在![]() 处得切线方程为
处得切线方程为![]() .
.
(2)因为![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
①若![]() ,则
,则![]() ,
,![]() 在
在![]() 上是单调增函数,
上是单调增函数,
所以![]() 在
在![]() 上至多一个零点,与题意不符合.
上至多一个零点,与题意不符合.
②若![]() ,令
,令![]() ,得
,得![]() .
.
|
|
|
|
|
| 0 |
|
|
| 极小值 |
|
(ⅰ)若![]() ,即
,即![]() 时,
时,![]() 有且仅有一个零点
有且仅有一个零点![]() ,与题意不符.
,与题意不符.
(ⅱ)若![]() ,即
,即![]() 时,
时,![]() ,
,![]() ,
,
又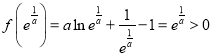 ,且
,且![]() 的图像在
的图像在![]() 上不间断,
上不间断,
所以存在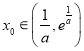 ,使得
,使得![]() .
.
此时,![]() 在
在![]() 恰有两个不同得零点
恰有两个不同得零点![]() 和
和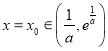 .
.
所以![]() 符合题意.
符合题意.
(ⅲ)若![]() ,即
,即![]() 时,
时,![]() .
.
令![]() ,
,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上是单调增函数,
上是单调增函数,![]() ,
,
所以![]() 在
在![]() 上是单调增函数,
上是单调增函数,![]() .
.
所以![]() ,且
,且![]() ,
,![]() 的图像在
的图像在![]() 上不间断,
上不间断,
所以存在![]() ,使得
,使得![]() .
.
此时,![]() 在
在![]() 恰有两个不同得零点
恰有两个不同得零点![]() 和
和![]() .
.
所以![]() 符合题意.
符合题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
(3)依题意![]() ,
,![]() .
.
则![]() ,令
,令![]() ,
,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上是单调增函数.
上是单调增函数.
要使得![]() 在
在![]() 上存在极值,
上存在极值,
则须满足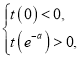 即
即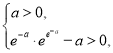
所以![]() ,
,![]() ,即
,即![]() .
.
由(2)可知,当![]() 时,
时,![]() ,
,
所以![]() ,
,![]() .
.
所以![]() ,即
,即![]() ,
,
所以![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面的问题中,并解决该问题.
这三个条件中任选一个,补充在下面的问题中,并解决该问题.
已知![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ______________,
______________,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改编自中国神话故事的动画电影《哪吒之魔童降世》自7月26日首映,在不到一个月的时间,票房收入就超过了38亿元,创造了中国动画电影的神话.小明和同学相约去电影院观看《哪吒之魔童降世》,影院的三个放映厅分别在7:30,8:00,8:30开始放映,小明和同学大约在7:40至8:30之间到达影院,且他们到达影院的时间是随机的,那么他们到达后等待的时间不超过10分钟的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是新中国成立七十周年,新中国成立以来,我国文化事业得到了充分发展,尤其是党的十八大以来,文化事业发展更加迅速,下图是从2013 年到 2018 年六年间我国公共图书馆业机构数(个)与对应年份编号的散点图(为便于计算,将 2013 年编号为 1,2014 年编号为 2,…,2018年编号为 6,把每年的公共图书馆业机构个数作为因变量,把年份编号从 1 到 6 作为自变量进行回归分析),得到回归直线![]() ,其相关指数
,其相关指数![]() ,给出下列结论,其中正确的个数是( )
,给出下列结论,其中正确的个数是( )

①公共图书馆业机构数与年份的正相关性较强
②公共图书馆业机构数平均每年增加13.743个
③可预测 2019 年公共图书馆业机构数约为3192个
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达
到达![]() 的位置,得到如图所示的四棱锥
的位置,得到如图所示的四棱锥![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
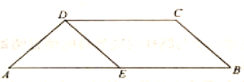
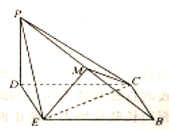
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,
,![]() 、
、![]() 、
、![]() 为抛物线
为抛物线![]() 上不同的三点.
上不同的三点.
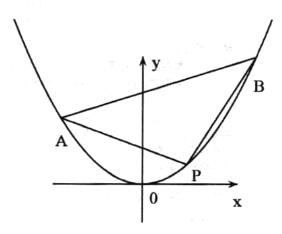
(1)当点![]() 的坐标为
的坐标为![]() 时,若直线
时,若直线![]() 过抛物线焦点
过抛物线焦点![]() 且斜率为
且斜率为![]() ,求直线
,求直线![]() 、
、![]() 斜率之积;
斜率之积;
(2)若![]() 为以
为以![]() 为顶点的等腰直角三角形,求
为顶点的等腰直角三角形,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出![]() 盒该产品获利润
盒该产品获利润![]() 元,未售出的产品,每盒亏损
元,未售出的产品,每盒亏损![]() 元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了
元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了![]() 盒该产品,以
盒该产品,以![]() (单位:盒,
(单位:盒,![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量,![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.

(1)根据直方图估计这个开学季内市场需求量![]() 的众数和平均数;
的众数和平均数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润![]() 不少于
不少于![]() 元的概率.
元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com