
【题目】已知函数![]() 是奇函数.
是奇函数.
![]() 求实数m,n的值;
求实数m,n的值;
![]() 若函数
若函数![]() 的定义域为
的定义域为![]() 判断函数
判断函数![]() 的单调性,并用定义证明;
的单调性,并用定义证明;![]() 是否存在实数t,使得关于x的不等式
是否存在实数t,使得关于x的不等式![]() 在
在![]() 上有解?若存在,求出t的取值范围;若不存在,说明理由.
上有解?若存在,求出t的取值范围;若不存在,说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x﹣a|, (Ⅰ)若a=4,求f(x)≤x的解集;
(Ⅱ)若f(x+1)>|2﹣a|对x∈(0,+∞)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 关于函数
关于函数![]() 的性质,有以下四个推断:
的性质,有以下四个推断:
①![]() 的定义域是
的定义域是![]() ; ②
; ②![]() 的值域是
的值域是![]() ;
;
③![]() 是奇函数; ④
是奇函数; ④![]() 是区间
是区间![]() 上的增函数.
上的增函数.
其中推断正确的题号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x+alnx(a∈R).
(1)讨论函数f(x)的单调性;
(2)若函数f(x)有两个极值点x1 , x2(x1<x2),且不等式f(x1)≥mx2恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强学生体质,学校组织体育社团,某宿舍有4人积极报名参加篮球和足球社团,每人只能从两个社团中选择其中一个社团,大家约定:每个人通过掷一枚质地均匀的骰子决定自己参加哪个社团,掷出点数为5或6的人参加篮球社团,掷出点数小于5的人参加足球社团.
(Ⅰ)求这4人中恰有1人参加篮球社团的概率;
(Ⅱ)用![]() 分别表示这4人中参加篮球社团和足球社团的人数,记随机变量
分别表示这4人中参加篮球社团和足球社团的人数,记随机变量![]() 为
为![]() 和
和![]() 的乘积,求随机变量
的乘积,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四个小动物换座位,开始是鼠、猴、兔、猫分别坐在 1,2,3,4 号位子上(如图), 第一次前后排动物互换座位,第二次左右列动物互换座位,.....,这样交替进行下去,那么第 2013 次互换座位后,小兔的座位对应的是( )

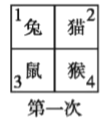
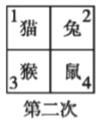
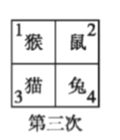
A. 编号 1 B. 编号 2 C. 编号 3 D. 编号 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com