
【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,E,F分别是AB,PD的中点,若PA=AD=3,CD=![]()
①求证:AF∥平面PCE
②求证:平面PCE⊥平面PCD
③求直线FC与平面PCE所成角的正弦值.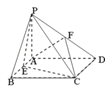
【答案】解:①取PC中点G,连接EG,FG;又由F为PD中点
∴FG![]()
![]() CD
CD
又∵AE![]()
![]() CD
CD
∴FG![]() AE,即可得四边形AEFG是平行四边形
AE,即可得四边形AEFG是平行四边形
∴AF∥EG
又AF平面PCE,EG平面PCE
∴AF∥平面PCE
②∵PA⊥平面ABCD
∴平面PAD⊥平面ABCD
∵CD⊥AD,∴CD⊥平面PAD,又AF在面PAD内
∴CD⊥AF
∵PA=AD,F为PD中点
∴AF⊥PD,又∵PD∩CD=D
∴AF⊥平面PCD
又∵EG∥AF
∴EG⊥平面PCD
又∵EG平面PCE
∴平面PCE⊥平面PCD
③在平面PCD内作FH⊥PC,则FH⊥平面PCE
∴∠FCH是FC与平面PCE所成的角
在△FCH中,![]() ,
,![]() ∴sin
∴sin![]()
∴直线FC与平面PCE所成角的正弦值为![]()
【解析】①根据有中点找中点做出辅助线,得到三组线线平行,得到四边形是一个平行四边形,得到线线平行,根据线面平行的判断得到结论.
②要证明面面垂直,根据证明面面垂直的判断需要找一条和两个平面垂直的一条直线,根据线面垂直的判断和性质,得到结论.
③在平面PCD内作FH⊥PC,则FH⊥平面PCE,得到∠FCH是FC与平面PCE所成的角,在这个可解的三角形中,求出角的正弦值.
【考点精析】根据题目的已知条件,利用向量语言表述面面的垂直、平行关系的相关知识可以得到问题的答案,需要掌握若平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,要证
,要证![]() ∥
∥![]() ,只需证
,只需证![]() ∥
∥![]() ,即证
,即证![]() ;要证
;要证![]() ,只需证
,只需证![]() ,即证
,即证![]() .
.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2mx+2m+3(m∈R),若关于x的方程f(x)=0有实数根,且两根分别为x1,x2,则(x1+x2)x1x2,的最大值为()
A. ![]() B. 2C. 3D.
B. 2C. 3D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三点O(0,0),A(﹣2,1),B(2,1),曲线C上任意一点M(x,y)满足| ![]() +
+ ![]() |=
|= ![]() (
( ![]() +
+ ![]() )+2.
)+2.
(1)求曲线C的方程;
(2)动点Q(x0 , y0)(﹣2<x0<2)在曲线C上,曲线C在点Q处的切线为直线l:是否存在定点P(0,t)(t<0),使得l与PA,PB都相交,交点分别为D,E,且△QAB与△PDE的面积之比是常数?若存在,求t的值.若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第![]() 届世界杯足球赛在俄罗斯进行,某校足球协会为了解该校学生对此次足球盛会的关注情况,随机调查了该校
届世界杯足球赛在俄罗斯进行,某校足球协会为了解该校学生对此次足球盛会的关注情况,随机调查了该校![]() 名学生,并将这
名学生,并将这![]() 名学生分为对世界杯足球赛“非常关注”与“一般关注”两类,已知这
名学生分为对世界杯足球赛“非常关注”与“一般关注”两类,已知这![]() 名学生中男生比女生多
名学生中男生比女生多![]() 人,对世界杯足球赛“非常关注”的学生中男生人数与女生人数之比为
人,对世界杯足球赛“非常关注”的学生中男生人数与女生人数之比为![]() ,对世界杯足球赛“一般关注”的学生中男生比女生少
,对世界杯足球赛“一般关注”的学生中男生比女生少![]() 人.
人.
(1)根据题意建立![]() 列联表,判断是否有
列联表,判断是否有![]() 的把握认为男生与女生对世界杯足球赛的关注有差异?
的把握认为男生与女生对世界杯足球赛的关注有差异?
(2)该校足球协会从对世界杯足球赛“非常关注”的学生中根据性别进行分层抽样,从中抽取![]() 人,再从这
人,再从这![]() 人中随机选出
人中随机选出![]() 人参与世界杯足球赛宣传活动,求这
人参与世界杯足球赛宣传活动,求这![]() 人中至少有一个男生的概率.
人中至少有一个男生的概率.
附:![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·全国卷Ⅲ文,18)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 的图像与
的图像与![]() 轴无交点,求
轴无交点,求![]() 的取值范围;
的取值范围;
(2)若方程![]() 在区间
在区间![]() 上存在实根,求
上存在实根,求![]() 的取值范围;
的取值范围;
(3)设函数![]() ,
,![]() ,当
,当![]() 时若对任意的
时若对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域相同的函数![]() 和
和![]() ,若存在实数
,若存在实数![]() ,
,![]() 使
使![]() ,则称函数
,则称函数![]() 是由“基函数
是由“基函数![]() ,
,![]() ”生成的.
”生成的.
(1)若函数![]() 是“基函数
是“基函数![]() ,
,![]() ”生成的,求实数
”生成的,求实数![]() 的值;
的值;
(2)试利用“基函数![]() ,
,![]() ”生成一个函数
”生成一个函数![]() ,且同时满足:①
,且同时满足:①![]() 是偶函数;②
是偶函数;②![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .求函数
.求函数![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com