
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 处取得极值,求实数
处取得极值,求实数![]() 的值;
的值;
(2)若函数![]() )在区间
)在区间![]() 上为增函数,求实数
上为增函数,求实数![]() 的取值范围;
的取值范围;
(3)若当![]() 时,方程
时,方程![]() 有实数根,求实数
有实数根,求实数![]() 的最大值.
的最大值.
【答案】(1) ![]() ;(2)
;(2) 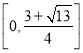 ;(3)0.
;(3)0.
【解析】试题分析:(1)函数在某一点处取得极值即该函数的导函数在该点的函数值为零;
(2)![]() 在
在![]() 上为增函数,
上为增函数, ![]() 在
在![]() 上恒成立,建立关于
上恒成立,建立关于![]() 的不等式,分类讨论求解即可;
的不等式,分类讨论求解即可;
(3)方程![]() 可转化为
可转化为![]() 在
在![]() 上有解,然后对
上有解,然后对![]() 的值域进行讨论,求出
的值域进行讨论,求出![]() 的取值范围即可.
的取值范围即可.
试题解析: (1) ![]()
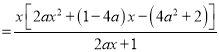 ,
,
因为函数![]() 在
在![]() 处取得极值,所以
处取得极值,所以![]() ,即
,即![]() ,解得
,解得![]() ,且经检验成立.
,且经检验成立.
(2)因为函数![]() 在区间
在区间![]() 上为增函数,
上为增函数,
所以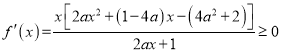 对
对![]() 恒成立.
恒成立.
讨论:
当![]() 时,
时, ![]() 对
对![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上为增函数,故
上为增函数,故![]() 符合题意.
符合题意.
当![]() 时,
时, ![]() ,所以
,所以![]() ,且
,且![]() 对
对![]() 上恒成立,
上恒成立,
令![]() ,其对称轴方程为
,其对称轴方程为![]() ,又因为
,又因为![]() ,所以
,所以![]() ,所以要使
,所以要使
![]() 对
对![]() 上恒成立,只要
上恒成立,只要![]() 即可,即
即可,即![]() ,所以
,所以![]() .
.
又因为![]() ,所以
,所以![]() .
.
综上,实数![]() 的取值范围为
的取值范围为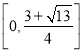 .
.
(3)当![]() 时,方程
时,方程![]() 可化为
可化为![]() .
.
所以![]() 在区间
在区间![]() 上有解.
上有解.
引入![]() ,令
,令![]() ,
,
则![]() ,
,
所以当![]() 时,
时, ![]() ,从而函数
,从而函数![]() 在
在![]() 上为增函数;
上为增函数;
当![]() 时,
时, ![]() ,从而函数
,从而函数![]() 在
在![]() 上为减函数,
上为减函数,
因此![]() .又
.又![]() ,所以当
,所以当![]() 时,
时, ![]() .
.
又![]() ,所以
,所以![]() ,因此当
,因此当![]() 时,
时, ![]() 取得最大0.
取得最大0.


科目:高中数学 来源: 题型:
【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差x (℃) | 10 | 11 | 13 | 12 | 8 |
发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程![]() =
=![]() x+
x+![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
附: 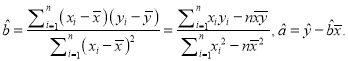
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间(满分100分,成绩不低于40分),现将成绩按如下方式分成6组:第一组![]() ;第二组
;第二组![]() ;……;第六组
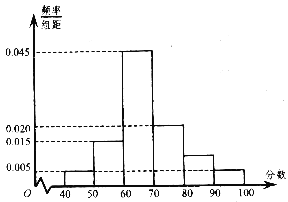
;……;第六组![]() ,并据此绘制了如图所示的频率分布直方图.
,并据此绘制了如图所示的频率分布直方图.
(Ⅰ)估计这次月考数学成绩的平均分和众数;
(Ⅱ)从成绩大于等于80分的学生中随机选2名,求至少有1名学生的成绩在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三个臭皮匠顶上一个诸葛亮,能顶得上吗?在一次有关“三国演义”的知识竞赛中,三个臭皮匠A、B、C能答对题目的概率分别为P(A)=![]() ,P(B)=
,P(B)=![]() ,P(C)=
,P(C)=![]() ,诸葛亮D能答对题目的概率为P(D)=
,诸葛亮D能答对题目的概率为P(D)=![]() ,如果将三个臭皮匠A、B、C组成一组与诸葛亮D比赛,答对题目多者为胜方,问哪方胜?
,如果将三个臭皮匠A、B、C组成一组与诸葛亮D比赛,答对题目多者为胜方,问哪方胜?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,现提供
,现提供![]() 的大致图象的8个选项:
的大致图象的8个选项:
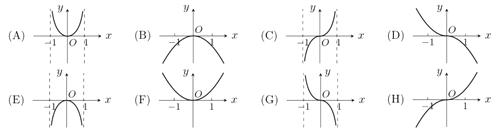
(1)请你作出选择,你选的是( );
(2)对于函数图像的判断,往往只需了解函数的基本性质.为了验证你的选择的正确性,请你解决
下列问题:
①![]() 的定义域是___________________;
的定义域是___________________;
②就奇偶性而言, ![]() 是______________________ ;
是______________________ ;
③当![]() 时,
时, ![]() 的符号为正还是负?并证明你的结论.
的符号为正还是负?并证明你的结论.
(解决了上述三个问题,你要调整你的选项,还来得及.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了纪念“中国红军长征90周年”,增强学生对“长征精神”的深刻理解,在全校组织了一次有关“长征”的知识竞赛,经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得20分,答错得0分.假设甲队中每人答对的概率均为![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为![]() ,
, ![]() ,
, ![]() ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用![]() 表示乙队的总得分.
表示乙队的总得分.
(1)求![]() 的分布列和均值;
的分布列和均值;
(2)求甲、乙两队总得分之和等于40分且甲队获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com