Question

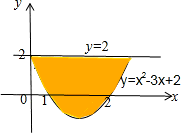
求曲线y=x²-3x+2与y=2围成的封闭图形的面积．

Answer 1

解：x²-3x+2=0，得x=1或x=2
x²-3x+2=2，得x=0，或 x=3．
所求面积S=∫₀³2dx-∫₀¹（x²-3x+2 ）dx-∫₂3（x²-3x+2 ）dx-∫₁2（x²-3x+2 ）dx=∫₀³2dx-∫₀ ³（x²-3x+2 ）dx=
分析：画出曲线y=x²-3x+2与y=2 围成的封闭图形，然后利用定积分表示区域面积，利用定积分的定义进行求解即可．
点评：本题考查定积分在求面积中的应用，要准确的用定积分表示面积．注意面积一定是正数，而定积分的值可为负数．