
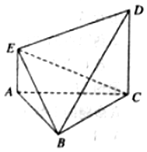
 如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.
如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.分析 (1)取BD边的中点F,BC的中点为G,连接AG,FG,EF,证明AG∥EF,由AG⊥平面BCD可知,EF⊥平面BCD,即可证明平面BDE⊥平面BCD;
(2)利用等体积方法,即可求三棱锥D-BCE的高.
解答  (1)证明:取BD边的中点F,BC的中点为G,连接AG,FG,EF,
(1)证明:取BD边的中点F,BC的中点为G,连接AG,FG,EF,
由题意可知,FG是△BCD的中位线
所以FG∥AE且FG=AE,即四边形AEFG为平行四边形,
所以AG∥EF
由AG⊥平面BCD可知,EF⊥平面BCD,又EF?面BDE,
故平面BDE⊥平面BCD;
(2)解:过B做BK⊥AC,垂足为K,因为AE⊥平面ABC,
所以BK⊥平面ACDE,且$BK=2×\frac{{\sqrt{3}}}{2}=\sqrt{3}$
所以V四棱锥B-ACDE=$\frac{1}{3}×\frac{1}{2}(1+2)$×$2×\sqrt{3}=\sqrt{3}$V三棱锥E-ABC=$\frac{1}{3}×\frac{1}{2}×2×$$\sqrt{3}×1=\frac{{\sqrt{3}}}{3}$
所以V三棱锥D-BCE=V四棱锥B-ACDE-V三棱锥E-ABC=$\sqrt{3}-\frac{{\sqrt{3}}}{3}=\frac{{2\sqrt{3}}}{3}$
因为AB=AC=2,AE=1,所以$BE=CE=\sqrt{5}$,又BC=2
所以${S_{△ECB}}=\frac{1}{2}×2×$$\sqrt{5-1}=2$
设所求的高为h,则由等体积法得$\frac{1}{3}×2×h$=$\frac{{2\sqrt{3}}}{3}$
所以$h=\sqrt{3}$.
点评 本题考查平面与平面垂直的证明和求三棱锥的高,解题时要认真审题,注意把空间几何问题等价转化为平面几何问题.


科目:高中数学 来源: 题型:填空题
 三条侧棱两两垂直的正三棱锥,其俯视图如图所示,主视图的边界是底边长为2的等腰三角形,则主视图的面积等于$\frac{{\sqrt{6}}}{3}$.
三条侧棱两两垂直的正三棱锥,其俯视图如图所示,主视图的边界是底边长为2的等腰三角形,则主视图的面积等于$\frac{{\sqrt{6}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
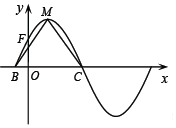 函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,M为最高点,该图象与y轴交于点F(0,$\sqrt{2}$),与x轴交于点B,C,且△MBC的面积为π.
函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,M为最高点,该图象与y轴交于点F(0,$\sqrt{2}$),与x轴交于点B,C,且△MBC的面积为π.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
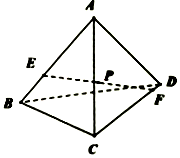 如图,在棱长为2的正四面体A-BCD中,E、F分别为直线AB、CD上的动点,且$|{EF}|=\sqrt{3}$.若记EF中点P的轨迹为L,则|L|等于$\frac{π}{4}$.(注:|L|表示L的测度,在本题,L为曲线、平面图形、空间几何体时,|L|分别对应长度、面积、体积.)
如图,在棱长为2的正四面体A-BCD中,E、F分别为直线AB、CD上的动点,且$|{EF}|=\sqrt{3}$.若记EF中点P的轨迹为L,则|L|等于$\frac{π}{4}$.(注:|L|表示L的测度,在本题,L为曲线、平面图形、空间几何体时,|L|分别对应长度、面积、体积.)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13.59% | B. | 15.73% | C. | 27.18% | D. | 31.46% |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com