
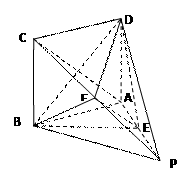
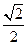
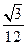
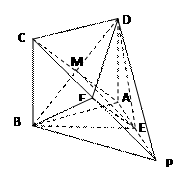
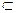 面EBD,∴PC∥面EBD
面EBD,∴PC∥面EBD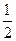 =3
=3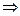 CB⊥PB ,∴PB⊥面ABCD,∴PB⊥MB,即MB为异面直线AC与PB间的垂线段
CB⊥PB ,∴PB⊥面ABCD,∴PB⊥MB,即MB为异面直线AC与PB间的垂线段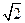
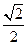
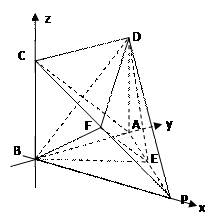
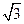 ,0,0),C(0,0,1),D(0,1,1)
,0,0),C(0,0,1),D(0,1,1)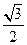 ,
,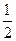 ,0)
,0)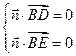
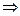
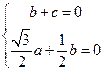
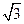 ,则b=-
,则b=-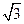 ,a=1
,a=1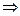 n=(1,-
n=(1,-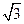 ,
,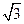 )
)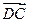 所成的角为
所成的角为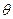
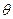 =
=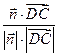 =
=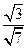
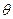 =
=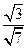
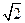 ,BE=1
,BE=1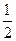 ×1×
×1×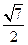 =
=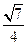
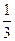 ×
×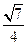 ×
×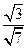 =
=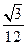


科目:高中数学 来源:不详 题型:单选题
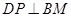 ,则点P的轨迹周长为( ).
,则点P的轨迹周长为( ).A.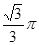 | B.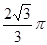 | C.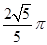 | D.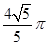 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
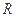 ,球面上
,球面上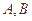 两点都在北纬45°圈上,它们的球面距离为
两点都在北纬45°圈上,它们的球面距离为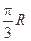 ,
,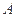 点在东经30°上,则
点在东经30°上,则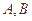 两点所在其纬线圈上所对应的劣弧的长度为( )
两点所在其纬线圈上所对应的劣弧的长度为( )A.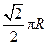 |
B.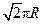 |
C.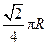 |
D.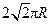 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com