
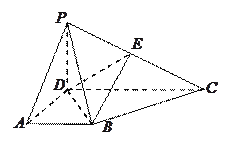
【题目】如图,在四棱锥![]() 中,
中,![]() ⊥平面
⊥平面![]() ,底面
,底面![]() 为梯形,
为梯形,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(Ⅰ)证明:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】【试题分析】(I)取![]() 的中点
的中点![]() ,连接
,连接![]() 通过证明四边形
通过证明四边形![]() 为平行四边形,由此证得
为平行四边形,由此证得![]() ,进而证明
,进而证明![]() 平面
平面![]() .(II)以
.(II)以![]() 为坐标原点建立空间直角坐标系,通过计算平面
为坐标原点建立空间直角坐标系,通过计算平面![]() 的法向量与直线
的法向量与直线![]() 的方向向量来计算线面角的正弦值.
的方向向量来计算线面角的正弦值.
【试题解析】
(Ⅰ)证明:设F为PD的中点,连接EF,FA.
因为EF为![]() 的中位线,所以EF∥CD,且EF=
的中位线,所以EF∥CD,且EF=![]() .
.
又AB∥CD,AB=2,所以AB![]() EF,故四边形ABEF为平行四边形,所以BE∥AF.
EF,故四边形ABEF为平行四边形,所以BE∥AF.
又 AF![]() 平面PAD,BE
平面PAD,BE![]() 平面PAD,所以BE∥平面PAD
平面PAD,所以BE∥平面PAD
(Ⅱ)解:设G为AB的中点,因为AD=AB,![]() ,所以
,所以![]() 为等边三角形,故DG⊥AB ;因为AB∥CD,所以DG⊥DC;又PD
为等边三角形,故DG⊥AB ;因为AB∥CD,所以DG⊥DC;又PD![]() 平面ABCD,所以PD,DG,CD两两垂直
平面ABCD,所以PD,DG,CD两两垂直
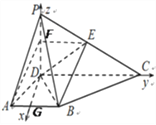
以D为坐标原点,![]() 为x轴、
为x轴、![]() 为
为![]() 轴、
轴、![]() 为
为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
设![]() 为平面DBE的一个法向量,则
为平面DBE的一个法向量,则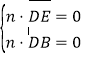 ,即
,即 ![]() ,
,
令![]() ,则
,则![]()
又![]() ,所以
,所以![]() ,
,
即直线PB与平面BDE所成角的正弦值为![]()


科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 且斜率为
且斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() :
:![]() 交椭圆
交椭圆![]() 于
于![]() 两点.
两点.
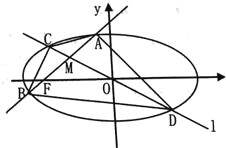
(1)求椭圆![]() 的方程;
的方程;
(2)求证:点![]() 在直线
在直线![]() 上;
上;
(3)是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】屠呦呦,第一位获得诺贝尔科学奖项的中国本土科学家,在2015年获得诺贝尔生理学或医学奖,理由是她发现了青蒿素.这种药品可以有效降低疟疾患者的死亡率,从青篙中提取的青篙素抗疟性超强,几乎达到100%.据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
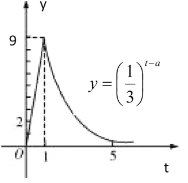
(Ⅰ)写出服药一次后y与t之间的函数关系式![]() ;
;
(Ⅱ)据进一步测定:每毫升血液中含药量不少于![]() 微克时,治疗有效,求服药一次后治疗有效的时间是多长?
微克时,治疗有效,求服药一次后治疗有效的时间是多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ,
,![]() ),记函数
),记函数![]() 的导函数为
的导函数为![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)是否存在实数![]() ,使得
,使得![]() 对任意正实数
对任意正实数![]() 恒成立?若存在,求出满足条件的实数
恒成立?若存在,求出满足条件的实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 上的动点
上的动点![]() 到坐标原点
到坐标原点![]() 的距离
的距离![]() 的最大值;
的最大值;
(Ⅱ)若曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且与
两点,且与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系![]() 中,平行于
中,平行于![]() 轴且过点
轴且过点![]() 的入射光线
的入射光线![]() 被直线
被直线![]() 反射,反射光线
反射,反射光线![]() 交
交![]() 轴于
轴于![]() 点,圆
点,圆![]() 过点
过点![]() ,且与
,且与![]() 、
、![]() 相切.
相切.
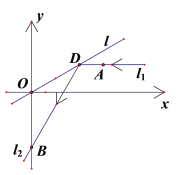
(Ⅰ)求![]() 所在直线的方程;
所在直线的方程;
(Ⅱ)求圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产一种产品,根据经验,其次品率![]() 与日产量
与日产量![]() (万件)之间满足关系,
(万件)之间满足关系, (其中
(其中![]() 为常数,且
为常数,且![]() ,已知每生产1万件合格的产品以盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如
,已知每生产1万件合格的产品以盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如![]() 表示每生产10件产品,有1件次品,其余为合格品).
表示每生产10件产品,有1件次品,其余为合格品).
(1)试将生产这种产品每天的盈利额![]() (万元)表示为日产量
(万元)表示为日产量![]() (万件)的函数;
(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com