
【题目】2019年全国“两会”,即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国会第二次会议,分别于2019年3月5日和3月3日在北京召开.为了了解哪些人更关注“两会”,某机构随机抽取了年龄在![]() 岁之间的200人进行调查,并按年龄绘制出频率分布直方图,如图.
岁之间的200人进行调查,并按年龄绘制出频率分布直方图,如图.
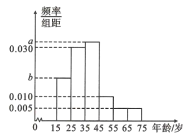
若把年龄在区间![]() ,
,![]() 内的人分别称为“青少年”“中老年”.经统计“青少年”和“中老年”的人数之比为
内的人分别称为“青少年”“中老年”.经统计“青少年”和“中老年”的人数之比为![]() .其中“青少年”中有40人关注“两会”,“中老年”中关注“两会”和不关注“两会”的人数之比为
.其中“青少年”中有40人关注“两会”,“中老年”中关注“两会”和不关注“两会”的人数之比为![]() .
.
(1)求图中![]() 的值.
的值.
(2)现采用分层抽样在![]() 和
和![]() 中随机抽取8人作为代表,从8人中任选2人,求2人都是“中老年”的概率.
中随机抽取8人作为代表,从8人中任选2人,求2人都是“中老年”的概率.
(3)根据已知条件,完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() %的把握认为“中老年”比“青少年”更加关注“两会”.
%的把握认为“中老年”比“青少年”更加关注“两会”.
关注 | 不关注 | 总计 | |
“青少年” | |||
“中老年” | |||
总计 |
附: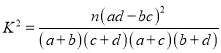 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(1)0.05;(2)![]() ;(3)列联表见解析;有99.9%的把握认为“中老年”比“青少年”更加关注“两会”
;(3)列联表见解析;有99.9%的把握认为“中老年”比“青少年”更加关注“两会”
【解析】
(1)由“青少年”和“中老年”的人数之比为![]() ,求出
,求出![]() 和
和![]() ,即可得到
,即可得到![]() 的值;
的值;
(2)由分层抽样求出在![]() 中抽取6人,在
中抽取6人,在![]() 中抽取2人,再由古典概型求出2人都是“中老年”的概率即可;
中抽取2人,再由古典概型求出2人都是“中老年”的概率即可;
(3)先求出![]() 列联表,再由公式计算出
列联表,再由公式计算出![]() ,比较即可得到结果.
,比较即可得到结果.
(1)由题意得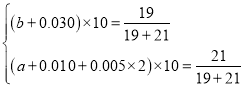 ,
,
解得![]() ,
,
所以![]() ;
;
(2)由题意得,在![]() 中抽取
中抽取![]() (人),
(人),
分别记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
在![]() 中抽取
中抽取![]() (人),分别记为
(人),分别记为![]() ,
,![]() .
.
则从8人中任选2人的全部基本事件有
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
共28种,其中所选的2人都是“中老年”的事件只有![]() 这1种,
这1种,
故2人都是“中老年”的概率![]() ;
;
(3)由题意得,抽取的200人中“青少年”共有![]() (人),
(人),
所以不关注两会的“青少年”共有![]() (人),
(人),
“中老年”中关注两会的人有![]()
![]() (人),
(人),
“中老年”中不关注两会的人有![]()
![]() (人),
(人),
所以![]() 列联表如下:
列联表如下:
关注 | 不关注 | 总计 | |
“青少年” | 40 | 55 | 95 |
“中老年” | 70 | 35 | 105 |
总计 | 110 | 90 | 200 |
所以![]() ,
,
所以有99.9%的把握认为“中老年”比“青少年”更加关注“两会”.


科目:高中数学 来源: 题型:
【题目】某快递公司为了解本公司快递业务情况,随机调查了100个营业网点,得到了这些营业网点2019年全年快递单数增长率x的频数分布表:

(1)分别估计该快递公司快递单数增长率不低于40%的营业网点比例和快递单数负增长的营业网点比例;
(2)求2019年该快递公司快递单数增长率的平均数和标准差的估计值(同一组中的数据用该组区间的中点值作为代表).(精确到0.01)参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 与
与![]() 轴交于
轴交于![]() 两点,且
两点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上的一个动点,且直线
上的一个动点,且直线![]() 与直线
与直线![]() 分别交于
分别交于![]() 两点.是否存在点
两点.是否存在点![]() 使得以
使得以![]() 为直径的圆经过点
为直径的圆经过点![]() ?若存在,求出点
?若存在,求出点![]() 的横坐标;若不存在,说明理由.
的横坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电动车生产企业,上年度生产电动车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1000辆.本年度为适应市场需求,计划提高产品档次,适度增加投入成本.若每辆车投入成本增加的比例为![]() ,则出厂价相应提高的比例为
,则出厂价相应提高的比例为![]() ,且当
,且当![]() 不超过0.5时,预计年销售量增加的比例为
不超过0.5时,预计年销售量增加的比例为![]() ,而当
,而当![]() 超过0.5时,预计年销售量不变.已知年利润=(出厂价-投入成本)×年销售量.则本年度预计的年利润
超过0.5时,预计年销售量不变.已知年利润=(出厂价-投入成本)×年销售量.则本年度预计的年利润![]() 与投入成本增加的比例
与投入成本增加的比例![]() 的关系式为______;为使本年度利润比上年有所增加,投入成本增加的比例
的关系式为______;为使本年度利润比上年有所增加,投入成本增加的比例![]() 的取值范围为______.
的取值范围为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆![]()
![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆
的圆是椭圆![]() 的“准圆”.若椭圆
的“准圆”.若椭圆![]() 的一个焦点为
的一个焦点为![]() ,其短轴上的一个端点到
,其短轴上的一个端点到![]() 的距离为
的距离为![]() .
.
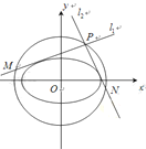
(1)求椭圆![]() 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点![]() 是椭圆
是椭圆![]() 的“准圆”上的动点,过点
的“准圆”上的动点,过点![]() 作椭圆的切线
作椭圆的切线![]() 交“准圆”于点
交“准圆”于点![]() .
.
①当点![]() 为“准圆”与
为“准圆”与![]() 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线![]() 的方程并证明
的方程并证明![]() ;
;
②求证:线段![]() 的长为定值.
的长为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com