
【题目】《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一.书中有一道这样的题目:把100个面包分给5个人,使每个人所得成等差数列,且使较大的三份之和的 ![]() 是较小的两份之和,问最小一份为( )
是较小的两份之和,问最小一份为( )
A.![]()
B.![]()
C.![]()
D.![]()
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】如图是某市2017年3月1日至16日的空气质量指数趋势图,空气质量指数![]() 小于
小于![]() 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于![]() 表示空气重度污染,某人随机选择3月1日至3月14日中的某一天到达该市.
表示空气重度污染,某人随机选择3月1日至3月14日中的某一天到达该市.
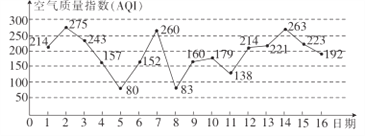
(1)若该人到达后停留![]() 天(到达当日算1天),求此人停留期间空气质量都是重度污染的概率;
天(到达当日算1天),求此人停留期间空气质量都是重度污染的概率;
(2)若该人到达后停留3天(到达当日算1天〉,设![]() 是此人停留期间空气重度污染的天数,求
是此人停留期间空气重度污染的天数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图.
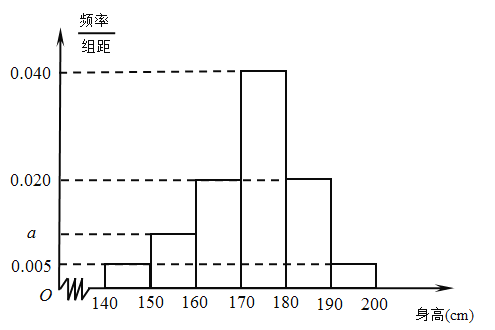
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)假设同组中的每个数据用该组区间的中点值代替,估计该市中学生中的全体男生的平均身高;
(Ⅲ)从该市的中学生中随机抽取一名男生,根据直方图中的信息,估计其身高在180 cm 以上的概率.若从全市中学的男生(人数众多)中随机抽取![]() 人,用
人,用![]() 表示身高在
表示身高在![]() 以上的男生人数,求随机变量
以上的男生人数,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义域为R的偶函数,当x≥0时,f(x)= 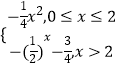 ,若关于x的方程[f(x)]2+af(x)+
,若关于x的方程[f(x)]2+af(x)+ ![]() =0,a∈R有且仅有8个不同实数根,则实数a的取值范围是
=0,a∈R有且仅有8个不同实数根,则实数a的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数fn(x)= ![]() x3﹣
x3﹣ ![]() (n+1)x2+x(n∈N*),数列{an}满足an+1=f'n(an),a1=3.
(n+1)x2+x(n∈N*),数列{an}满足an+1=f'n(an),a1=3.
(1)求a2 , a3 , a4;
(2)根据(1)猜想数列{an}的通项公式,并用数学归纳法证明;
(3)求证: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为S(x),则函数S(x)的导函数S′(x)的图象大致是( ) 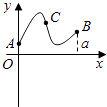
A.
B.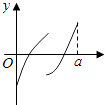
C.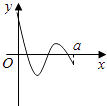
D.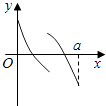
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,数列{bn},{cn}满足 (n+1) bn=an+1![]() ,(n+2) cn=
,(n+2) cn=![]() ,其中n∈N*.
,其中n∈N*.
(1)若数列{an}是公差为2的等差数列,求数列{cn}的通项公式;
(2)若存在实数λ,使得对一切n∈N*,有bn≤λ≤cn,求证:数列{an}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家公司计划生产某种小型产品的月固定成本为1万元,每生产1万件需要再投入2万元,设该公司一个月内生产该小型产品x万件并全部销售完,每万件的销售收入为4﹣x万元,且每万件国家给予补助2e﹣ ![]() ﹣
﹣ ![]() 万元.(e为自然对数的底数,e是一个常数)
万元.(e为自然对数的底数,e是一个常数)
(1)写出月利润f(x)(万元)关于月产量x(万件)的函数解析式
(2)当月产量在[1,2e]万件时,求该公司在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生成量值(万件).(注:月利润=月销售收入+月国家补助﹣月总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 a∈R,函数 f(x)=a﹣ ![]() .
.
(1)证明:f(x)在(﹣∞,+∞)上单调递增;
(2)若f(x)为奇函数,求:
①a的值;
②f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com