
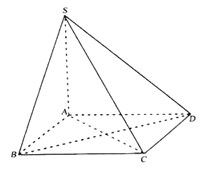
【题目】已知四棱锥![]() 的底面
的底面![]() 是正方形,
是正方形,![]() 底面
底面![]() .
.
(1)求证:直线![]() 平面
平面![]() ;
;
(2)当![]() 的值为多少时,二面角
的值为多少时,二面角![]() 的大小为
的大小为![]() ?
?
【答案】(1)证明见解析;(2)1.
【解析】分析:(1)由线面垂直的性质可得![]() ,由正方形的性质可得
,由正方形的性质可得![]() ,由线面垂直的判定定理可证
,由线面垂直的判定定理可证![]() 平面
平面![]() ;(2)设
;(2)设![]() ,以
,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,设
,设![]() ,分别利用向量垂直数量积为零列方程组,求出平面
,分别利用向量垂直数量积为零列方程组,求出平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,由空间向量夹角余弦公式列方程可得结果.
的法向量,由空间向量夹角余弦公式列方程可得结果.
详解:(1)证明:∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵四边形![]() 是正方形,∴
是正方形,∴![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() .
.
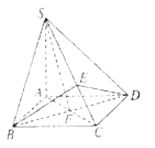
(2)解:设![]() ,以
,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,为计算方便,不妨设
,为计算方便,不妨设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则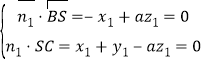 ,
,
令![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,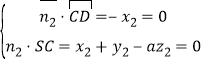 ,
,
令![]() ,又
,又![]() ,则
,则![]() ,∴
,∴![]() .
.
要使二面角![]() 的大小为
的大小为![]() ,必有
,必有![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
即当![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某同学用收集到的6组数据对![]() 制作成如图所示的散点图(点旁的数据为该点坐标),并由最小二乘法计算得到回归直线
制作成如图所示的散点图(点旁的数据为该点坐标),并由最小二乘法计算得到回归直线![]() 的方程:
的方程:![]() ,相关系数为
,相关系数为![]() ,相关指数为
,相关指数为![]() ;经过残差分析确定点
;经过残差分析确定点![]() 为“离群点”(对应残差过大的点),把它去掉后,再用剩下的5组数据计算得到回归直线
为“离群点”(对应残差过大的点),把它去掉后,再用剩下的5组数据计算得到回归直线![]() 的方程:
的方程:![]() ,相关系数为
,相关系数为![]() ,相关指数为
,相关指数为![]() .则以下结论中,不正确的是( )
.则以下结论中,不正确的是( )

A. ![]() ,
,![]() B.
B. ![]() ,
,![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 为梯形,
为梯形,![]() 平面
平面![]() ,
,![]() ,
,
![]() 为
为![]() 中点.
中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若存在,找出具体位置,并进行证明:若不存在,请分析说明理由.
?若存在,找出具体位置,并进行证明:若不存在,请分析说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 是抛物线
是抛物线![]() 的准线,直线
的准线,直线![]() ,且
,且![]() 与抛物线
与抛物线![]() 没有公共点,动点
没有公共点,动点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 到直线
到直线![]() 和
和![]() 的距离之和的最小值等于2.
的距离之和的最小值等于2.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)点![]() 在直线
在直线![]() 上运动,过点
上运动,过点![]() 做抛物线
做抛物线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,在平面内是否存在定点
,在平面内是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,请求出定点
恒成立?若存在,请求出定点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市![]() 年
年![]() 月
月![]() 日至
日至![]() 日的空气质量指数趋势图,某人随机选择
日的空气质量指数趋势图,某人随机选择![]() 年
年![]() 月
月![]() 日至
日至![]() 月
月![]() 日中的某一天到达该市,并停留
日中的某一天到达该市,并停留![]() 天.
天.
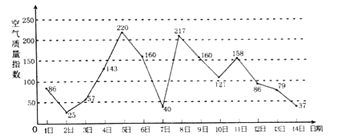
(1)求此人到达当日空气质量指数大于![]() 的概率;
的概率;
(2)设![]() 是此人停留期间空气质量指数小于
是此人停留期间空气质量指数小于![]() 的天数,求
的天数,求![]() 的分布列与数学期望;
的分布列与数学期望;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+ax2
(1)讨论f(x)的单调性;
(2)设a>1,若对任意x1 , x2∈(0,+∞),恒有|f(x1)﹣f(x2)|≥4|x1﹣x2|,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:

(1)三棱锥A′-BC′D的表面积与正方体表面积的比值;
(2)三棱锥A′-BC′D的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一张坐标纸上已作出圆![]() 及点
及点![]() ,折叠此纸片,使
,折叠此纸片,使![]() 与圆周上某点
与圆周上某点![]() 重合,每次折叠都会留下折痕,设折痕与直线
重合,每次折叠都会留下折痕,设折痕与直线![]() 的交点为
的交点为![]() ,令点
,令点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.

(1)求曲线![]() 的方程;
的方程;
(2)若直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 、
、![]() 两点,且直线
两点,且直线![]() 与以
与以![]() 为直径的圆相切,若
为直径的圆相切,若![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com