
素材2:f(x)+f(x-![]() )≤0;
)≤0;
素材3:函数y=f(x)(x∈R且x≠0)对任意非零实数x1、x2,恒有f(x1x2)=f(x1)+f(x2).
先将上面的素材构建成一个问题,然后再解答.
构建问题:设函数y=f(x)(x∈R且x≠0)对任意非零实数x1、x2,恒有f(x1x2)=f(x1)+f(x2),
(1)求证:y=f(x)是偶函数;
(2)已知y=f(x)为(0,+∞)上的增函数,求适合f(x)+f(x-![]() )≤0的x的取值范围.
)≤0的x的取值范围.
(1)证明:∵f(x1x2)=f(x1)+f(x2)(x1x2≠0),
∴f(1)=f(1)+f(1)=2f(1).
∴f(1)=0.
∴f(1)=f(-1)+f(-1)=2f(-1).
∴2f(-1)=0,即f(-1)=0.
对任意的x≠0,都有f(-x)=f(-1)+f(x)=f(x),
∴f(x)为偶函数.
(2)解析:∵f(x1x2)=f(x1)+f(x2)(x1x2≠0),
∴f(x)+f(x-![]() )=f(x2-
)=f(x2-![]() x).
x).
∵f(x)+f(x-![]() )≤0,
)≤0,
∴f(x2-![]() x)≤0.
x)≤0.
∵f(x)为偶函数且f(1)=0,
∴f(|x2-![]() x|)≤f(1).
x|)≤f(1).
∵f(x)在(0,+∞)上是增函数,
∴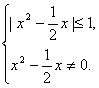
∴![]() ≤x≤
≤x≤![]() 且x≠0,x≠
且x≠0,x≠![]() .
.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com