
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 既有一个极小值又有一个极大值,求
既有一个极小值又有一个极大值,求![]() 的取值范围;
的取值范围;
(3)若存在![]() ,使得当
,使得当![]() 时,
时, ![]() 的值域是
的值域是![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() .
.
【解析】试题分析:
(1)当![]() 时,
时, ![]() ,利用导函数研究函数的单调性可得函数
,利用导函数研究函数的单调性可得函数![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ;
;
(2)求解导函数有![]() ,令
,令![]() ,则方程
,则方程![]() 必有两个不等的正根,据此结合二次方程根的分布可得实数
必有两个不等的正根,据此结合二次方程根的分布可得实数![]() 的取值范围是
的取值范围是![]() ;
;
(3)求解导函数, ![]() ,分类讨论
,分类讨论![]() 时和
时和![]() 时两种情况可得
时两种情况可得![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时, ![]() ,令
,令![]() 得
得![]() ,
,
当![]() 时
时![]() ,当
,当![]() 时,
时, ![]() ,
,
∴函数![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ;
;
(2)![]() ,则
,则![]() ,
,
令![]() ,若函数
,若函数![]() 有两个极值点,
有两个极值点,
则方程![]() 必有两个不等的正根,
必有两个不等的正根,
设两根为![]() ,于是
,于是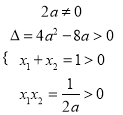 ,解得
,解得![]() ,
,
当![]() 时,
时, ![]() 有两个不相等的正实根,设为
有两个不相等的正实根,设为![]() ,不妨设
,不妨设![]() ,
,
则![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 在
在![]() 上为减函数;
上为减函数;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上为增函数;
上为增函数;
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上为减函数.
上为减函数.
由此, ![]() 是函数
是函数![]() 的极小值点,
的极小值点, ![]() 是函数
是函数![]() 的极大值点.符合题意 .
的极大值点.符合题意 .
综上,所求实数![]() 的取值范围是
的取值范围是![]() ;
;
(3)![]() ,
,
①当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() 的
的![]() 上为减函数;
上为减函数;
当![]() 时,
时, ![]() 在
在![]() 上为增函数,
上为增函数,
所以,当![]() 时,
时, ![]() 的值域是
的值域是![]() ,
,
不符合题意.
②当![]() 时,
时, 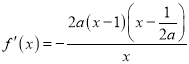 ,
,
(i)当![]() ,即
,即![]() 时,当
时,当![]() 变化时,
变化时, ![]() 的变化情况如下:
的变化情况如下:
|
|
|
| 1 |
|
| - | 0 | + | 0 | - |
| 减函数 | 极小值 | 增函数 | 极大值 | 减函数 |
若满足题意,只需满足![]() ,即
,即![]() ,
,
整理得![]() ,令
,令![]() ,
,
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上为增函数,
上为增函数,
即当![]() 时,
时, ![]() ,
,
可见,当![]() 时,
时, ![]() 恒成立,
恒成立,
故当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ;
;
所以![]() 满足题意.
满足题意.
(ii)当![]() ,即
,即![]() 时,
时, ![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
所以![]() 在
在![]() 上为减函数,从而
上为减函数,从而![]() 在
在![]() 上为减函数,
上为减函数,
符合题意;
(iii)当![]() ,即
,即![]() 时,当
时,当![]() 变化时,
变化时, ![]() 的变化情况如下表:
的变化情况如下表:
|
| 1 |
|
|
|
| - | 0 | + | 0 | - |
| 减函数 | 极小值0 | 增函数 | 极大值 | 减函数 |
若满足题意,只需满足![]() ,且
,且![]() (若
(若![]() ,不符合题意),
,不符合题意),
即![]() ,且
,且![]() ,
,
又![]() ,所以
,所以![]() ,此时,
,此时, ![]() ,
,
综上, ![]() ,
,
所以,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某重点高中拟把学校打造成新型示范高中,为此制定了学生“七不准”,“一日三省十问”等新的规章制度.新规章制度实施一段时间后,学校就新规章制度随机抽取部分学生进行问卷调查,调查卷共有10个问题,每个问题10分,调查结束后,按分数分成5组:[50,60),60,70),[70,80),[80,90),[90,100],并作出频率分布直方图与样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据). 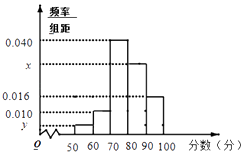
(1)求样本容量n和频率分布直方图中的x、y的值;
(2)在选取的样本中,从分数在70分以下的学生中随机抽取2名学生进行座谈会,求所抽取的2名学生中恰有一人得分在[50,60)内的概率.
5 | 3 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化妆品生产企业为了占有更多的市场份额,拟在2010年世博会期间进行一系列促销活动,经过市场调查和测算,化妆品的年销量x万件与年促销费t万元之间满足3﹣x与t+1成反比例,如果不搞促销活动,化妆品的年销量只能是1万件,已知2010年生产化妆品的设备折旧、维修等固定费用为3万元,每生产1万件化妆品需要再投入32万元的生产费用,若将每件化妆品的售价定为:其生产成本的150%与平均每件促销费的一半之和,则当年生产的化妆品正好能销完.
(1)将2010年利润y(万元)表示为促销费t(万元)的函数;
(2)该企业2010年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入﹣生产成本﹣促销费,生产成本=固定费用+生产费用)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将甲、乙两颗骰子先后各抛一次,a、b分别表示抛掷甲、乙两颗骰子所出现的点数﹒图中三角形阴影部分的三个顶点为(0,0)、(4,0)和(0,4). 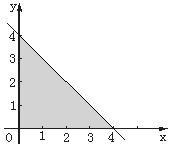
(1)若点P(a,b)落在如图阴影所表示的平面区域(包括边界)的事件记为A,求事件A的概率;
(2)若点P(a,b)落在直线x+y=m(m为常数)上,且使此事件的概率P最大,求m和P的值﹒
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和是Sn , 且Sn+ ![]() an=1(n∈N*).
an=1(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=log4(1﹣Sn+1)(n∈N*),Tn= ![]() +
+ ![]() +…+
+…+ ![]() ,求使Tn≥
,求使Tn≥ ![]() 成立的最小的正整数n的值.
成立的最小的正整数n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+(y﹣2)2=25及直线l:(2m+1)x+(m+1)y=7m+4.(m∈R)
(1)证明:不论m取什么实数,直线l与圆C恒相交;
(2)求直线l与圆C所截得的弦长的最短长度及此时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com