
| A. | (4,$\frac{2}{3}$π) | B. | (-4,$\frac{2}{3}$π) | C. | (-4,$\frac{1}{3}$π) | D. | (4,$\frac{1}{3}$π) |
分析 由x=ρcosθ,y=ρsinθ,可得tanθ=$\frac{y}{x}$,ρ=$\sqrt{{x}^{2}+{y}^{2}}$.(θ由(x,y)所在象限确定).将点的直角坐标(-2,2$\sqrt{3}$),代入可得ρ,θ.
解答 解:由x=ρcosθ,y=ρsinθ,
可得tanθ=$\frac{y}{x}$,ρ=$\sqrt{{x}^{2}+{y}^{2}}$.(θ由(x,y)所在象限确定).
由点的直角坐标(-2,2$\sqrt{3}$),
可得x=-2,y=2$\sqrt{3}$,
可得ρ=$\sqrt{4+12}$=4,
tanθ=$\frac{2\sqrt{3}}{-2}$=-$\sqrt{3}$.
即有θ=$\frac{2π}{3}$
则所求极坐标为(4,$\frac{2π}{3}$).
故选:A.
点评 本题考查极坐标和直角坐标的互化,注意运用tanθ=$\frac{y}{x}$,ρ=$\sqrt{{x}^{2}+{y}^{2}}$.(θ由(x,y)所在象限确定).考查运算能力,属于基础题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:选择题
| A. | 小指 | B. | 中指 | C. | 食指 | D. | 大拇指 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
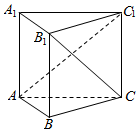 三棱柱ABC-A1B1C1中,△ABC是等边三角形,AA1⊥底面ABC,AB=2,AA1=$\sqrt{2}$,则异面直线AC1与B1C所成的角的大小是( )
三棱柱ABC-A1B1C1中,△ABC是等边三角形,AA1⊥底面ABC,AB=2,AA1=$\sqrt{2}$,则异面直线AC1与B1C所成的角的大小是( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com