
【题目】已知过定点![]() 且与直线
且与直线![]() 垂直的直线与
垂直的直线与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,点
,点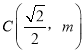 满足
满足![]() .
.
(1)若以原点为圆心的圆![]() 与
与![]() 有唯一公共点,求圆
有唯一公共点,求圆![]() 的轨迹方程;
的轨迹方程;
(2)求能覆盖![]() 的最小圆的面积;
的最小圆的面积;
(3)在(1)的条件下,点![]() 在直线
在直线![]() 上,圆
上,圆![]() 上总存在两个不同的点
上总存在两个不同的点![]() 使得
使得![]()
![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
(1)![]() ,得
,得![]() 在直线
在直线![]() 上,求出
上,求出![]() ,确定圆的半径则方程可求
,确定圆的半径则方程可求
(2)由几何关系得能覆盖三角形ABC的最小圆是以AB为直径的圆,计算![]() ,则圆的面积可求
,则圆的面积可求
(3)由![]() ,则有OP与MN互相垂直平分,得
,则有OP与MN互相垂直平分,得![]() 利用点在直线上得
利用点在直线上得![]() 的不等式求解
的不等式求解
(1)因为![]() ,所以
,所以![]() 在线段
在线段![]() 的垂直平分线上,即在直线
的垂直平分线上,即在直线![]() 上,
上,
故![]()
以原点为圆心的圆![]() 与
与![]() 有唯一公共点,
有唯一公共点,
此时圆的半径
故:圆![]() 的方程为
的方程为![]()
(2)由于三角形ABC为钝角三角形且AB为最长边,故能覆盖三角形ABC的最小圆是以AB为直径的圆
由于点![]() ,所以
,所以![]()
故该圆的半径为![]()
所以能覆盖该三角形的最小圆面积![]()
(3)![]() (O为坐标原点),则有OP与MN互相垂直平分,
(O为坐标原点),则有OP与MN互相垂直平分,
所以圆心到直线MN的距离小于1.即又![]()
又![]() ,代入(1)得
,代入(1)得
![]()
所以实数![]() 的取值范围为
的取值范围为![]()


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,过定点
,过定点![]() 作不垂直于x轴的直线
作不垂直于x轴的直线![]() ,交抛物线于A,B两点.
,交抛物线于A,B两点.
(1)设O为坐标原点,求证:![]() 为定值;
为定值;
(2)设线段![]() 的垂直分线与x轴交于点
的垂直分线与x轴交于点![]() ,求n的取值范围;
,求n的取值范围;
(3)设点A关于x轴的对称点为D,求证:直线![]() 过定点,并求出定点的坐标.
过定点,并求出定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCED中,BE⊥CD,平面ABED⊥平面BCE.在梯形ABED中,AB∥DE,BE⊥AB.DE=BE=CE=2AB,M是BC的中点,点N在线段DE上,且满足DN=![]() DE.
DE.

(1)求证:MN∥平面ACD;
(2)若AB=2,求点N到平面ABC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式组![]() 所表示的平面区域为
所表示的平面区域为![]() ,其面积为
,其面积为![]() .①若
.①若![]() ,则
,则![]() 的值唯一;②若
的值唯一;②若![]() ,则
,则![]() 的值有2个;③若
的值有2个;③若![]() 为三角形,则
为三角形,则![]() ;④若
;④若![]() 为五边形,则
为五边形,则![]() .以上命题中,真命题的个数是( )
.以上命题中,真命题的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是两条异面直线,直线
是两条异面直线,直线![]() 与
与![]() 都垂直,则下列说法正确的是( )
都垂直,则下列说法正确的是( )
A. 若![]() 平面
平面![]() ,则
,则![]()
B. 若![]() 平面
平面![]() ,则
,则![]() ,
,![]()
C. 存在平面![]() ,使得
,使得![]() ,
,![]() ,
,![]()
D. 存在平面![]() ,使得
,使得![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在等腰梯形![]() 中,
中,![]() 分别为
分别为![]() 的中点
的中点![]()
![]() 为
为![]() 中点,现将四边形
中点,现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到如图②所示的多面体,在图②中.
,得到如图②所示的多面体,在图②中. 
(1)证明:![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(-1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(1)将红色卡片和蓝色卡片分别放在两个袋中,然后从两个袋中各取一张卡片,求两张卡片数字之积为偶数的概率
(2)将五张卡片放在一个袋子中,从中任取两张,求两张卡片颜色不同的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com