
分析 (Ⅰ)求出汽车从甲地匀速行驶到乙地所用时间,根据货车每小时的运输成本(以元为单位)由可变部分和固定部分组成,可得全程运输成本,及函数的定义域;
(Ⅱ)利用基本不等式可得结论.
解答 解:(Ⅰ)可变成本为$\frac{1}{4}{v^2}$,固定成本为a元,所用时间为$\frac{1000}{v}$,
∴$y=\frac{1000}{v}({\frac{1}{4}{v^2}+a})$,即$y=1000({\frac{1}{4}v+\frac{a}{v}})$.
定义域为(0,80];
(Ⅱ)$y=1000({\frac{v}{4}+\frac{400}{v}})≥1000•2\sqrt{100}=20000$,
当且仅当$\frac{v}{4}=\frac{400}{v}$,即v=40时等号成立,
∴当v=40时,ymin=20000
答:当火车以40km/h的速度行驶,全程运输成本最小.
点评 本题考查函数模型的构建,考查基本不等式的运用,解题的关键是构建函数模型,利用基本不等式求最值.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:选择题
已知直线 的方向向量
的方向向量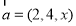 ,直线
,直线 的方向向量
的方向向量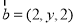 ,若
,若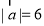 ,且
,且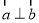 ,则
,则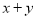 的值是( )
的值是( )
A.-3或1 B.3或-1 C.-3 D.1
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱的侧面积为16π
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱的侧面积为16π查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com