练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

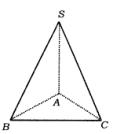
    如图所示，已知SA、SB、SC是由点S引出的不共面的三条线段，＝45°，＝60°，＝90°，求证：．

    答案：
    解析：

    设SA=a．如图所示，过A作AE⊥SC，垂足为E，则由∠ASC=45º知，．

        在Rt△SAB中，，SA=a．

        连结BE，在△SBE中，由余弦定理，得

        BE2=SB2+SE2－2SB·SEcos60º，

       

        ，

        在△BAE中，有AB2+AE2=a2+=BE2，根据勾股定理的逆定理，∠BAE=90º．即AB⊥AE，

        又AB⊥SA，∴AB⊥平面SAC．

    ∵SC平面SAC，∴AB⊥SC．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

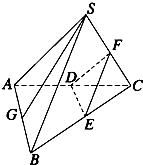    如图所示，已知S是正三角形ABC所在平面外的一点，且SA=SB=SC，SG为△SAB上的高，D、E、F分别是AC、BC、SC的中点，试判断SG与平面DEF的位置关系，并给予证明．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    如图所示，已知SA、SB、SC是由点S引出的不共面的三条线段，＝45°，＝60°，＝90°，求证：．

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省高一上学期期末模拟数学试卷（解析版） 题型：解答题

    （本小题满分12分）

    如图所示，已知S是正三角形ABC所在平面外的一点，且SA=SB=SC，SG为△SAB上的高，D、E、F分别是AC、BC、SC的中点，试判断SG与平面DEF的位置关系，并给予证明.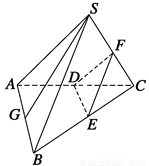

     

    查看答案和解析>>

    科目：高中数学 来源：2014届辽宁瓦房店高级中学高二上期中考试理科数学试卷（解析版） 题型：解答题

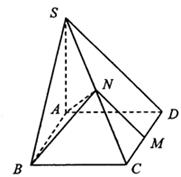
    （本题满分12分）如图所示，已知四棱锥S—ABCD的底面ABCD是矩形，M、N分别是CD、SC的中点，SA⊥底面ABCD，SA=AD=1，AB=.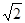

    （1）求证：MN⊥平面ABN；（2）求二面角A—BN—C的余弦值

     

    查看答案和解析>>

    同步练习册答案