练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．求下列各式的值：
    （1）$\frac{1+tan75°}{1-tan75°}$；
    （2）tan17°+tan28°+tan17°tan28°．

    分析 （1）利用tan45°=1和两角和的正切公式化简$\frac{1+tan75°}{1-tan75°}$即可．
    （2）把tan17°+tan28°=tan（17°+28°）（1-tan17°tan28°）代入所给的式子，化简可得结果．

    解答 解：（1）$\frac{1+tan75°}{1-tan75°}$=$\frac{tan45°+tan75°}{1-tan45°tan75°}$=tan（45°+75°）=tan120°=-$\sqrt{3}$．
    （2）tan17°+tan28°+tan17°tan28°=tan（17°+28°）（1-tan17°tan28°）+tan17°tan28°=tan45°=1．

    点评 本题考查两角和的正切公式，以及特殊角的正切值：“1”的代换问题，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    13．在△ABC中，a，b，c分别为内角A，B，C的对边，C为锐角且asinA=bsinBsinC，$b=\sqrt{2}a$．
    （1）求C的大小；
    （2）求$\frac{c^2}{a^2}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．若正数a，b满足ab=a+b+3，则ab的取值范围是（　　）
    A．（3，9]B．[9，+∞）C．[9，27]D．[27，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．盒子中有大小形状完全相同的4个红球和3个白球，从中不放回的一次摸出两个球，在第一次摸出的是红球的前提下，第二次也摸出红球的概率为（　　）
    A．$\frac{2}{7}$B．$\frac{2}{3}$C．$\frac{1}{2}$D．$\frac{1}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

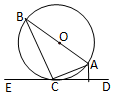    19．如图，AB是圆O的直径，直线CE和圆O相切于点C，AD⊥CE于D，若AD=1，∠ABC=30°，则圆O的面积是（　　）
    A．4πB．6πC．8πD．16π

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．设方程$\frac{x^2}{m+2}-\frac{y^2}{2m-1}=1$表示双曲线，则实数m的取值范围是（-∞，-2）∪（$\frac{1}{2}$，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．在北纬60°的纬度圈上，有甲、乙两地，两地间纬度圈上的弧长等于$\frac{πR}{4}$（R为地球半径），则这两地的球面距离是R$arccos\frac{3}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知全集U=R，集合M=$\left\{{x\left|{\frac{2-x}{x+3}}\right.＜0}\right\}$，则∁RM={x|-3≤x≤2}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．求分别满足下列条件的直线方程，并化为一般式
    （1）经过点（-1，3），且斜率为-3；
    （2）经过两点A（0，4）和B（4，0）；
    （3）经过点（2，-4）且与直线3x-4y+5=0平行；
    （4）经过点（1，2），且与直线x-y+5=0垂直．

    查看答案和解析>>

    同步练习册答案