
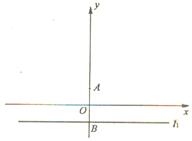
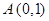 ,直线
,直线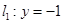 交
交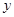 轴于点
轴于点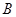 ,记过点
,记过点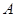 且与直线
且与直线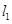 相切的圆的圆心为点
相切的圆的圆心为点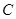 .
.
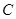 的轨迹
的轨迹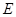 的方程;
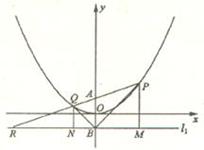
的方程;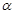 的直线
的直线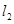 过点
过点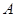 ,交轨迹
,交轨迹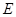 于两点
于两点 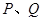 ,交直线
,交直线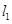 于点
于点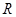 .若
.若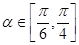 ,求
,求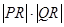 的最小值.
的最小值.
 ………6分
………6分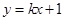 ,与抛物线方程联立消去y得x2-4kx-4=0.
,与抛物线方程联立消去y得x2-4kx-4=0.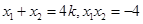 .
. .
.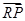 ·
·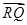 =(x1+
=(x1+ ,y1+1)·(x2+
,y1+1)·(x2+ ,y2+1)
,y2+1) )(x2+
)(x2+ )+(kx1+2 )(kx2+ 2)
)+(kx1+2 )(kx2+ 2) +2 k)( x1+x2)+
+2 k)( x1+x2)+ 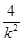 +4
+4 +2k)+
+2k)+ 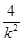 +4
+4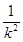 )+8,
)+8,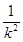 ≥2,当且仅当k2=1时取到等号.
≥2,当且仅当k2=1时取到等号. ,
,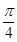 ],k∈[
],k∈[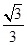 ,1],∴上述不等式中等号能取到.
,1],∴上述不等式中等号能取到.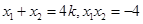 .
.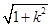 |x1-xR|·
|x1-xR|·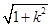 |x2-xR|
|x2-xR| )(x2+
)(x2+ ),
),

 金博士一点全通系列答案
金博士一点全通系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com