Question

（2009•宁波模拟）在单位正方体AC₁中，点E、F分别是棱BC、CD的中点．
（Ⅰ）求证：D₁E⊥平面AB₁F；
（Ⅱ）求三棱锥E-AB₁F的体积；
（Ⅲ）设直线B₁E、B₁D₁与平面AB₁F所成的角分别为α、β，求cos（α+β）．

Answer 1

分析：（Ⅰ）线根据其为正方体可得AB₁⊥D₁E以及AF⊥D₁D；再根据Rt△ADF与Rt△DCE全等得到AF⊥DE；可证AF⊥平面D₁DE进而得AF⊥D₁E，即可证明结论成立．
（Ⅱ）先求出三角形AEF的面积，再根据体积相等把所求问题转化为VB 1-AEF即可．
（Ⅲ）先根据DE⊥平面AB₁F得到∠EB₁D₁=α+β；再分两部分求，先求出两个角的三角函数值，再由余弦的和角公式求解即可．

解答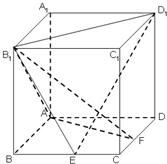：（Ⅰ）证明：在正方体AC₁中，连A₁B，D₁C．
AB₁⊥平面A₁BCD₁，D₁E?平面A₁BCD₁⇒AB₁⊥D₁E…（2分）
连接DE，则Rt△ADF与Rt△DCE全等⇒AF⊥DE
D₁D⊥平面ABCD
AF?平面ABCD⇒AF⊥D₁D
DE∩D₁D=D
⇒AF⊥平面D₁DE⇒AF⊥D₁E
又AB₁∩AF=A，故D₁E⊥平面AB₁F．     …（5分）
（Ⅱ）由（Ⅰ）知，E为棱BC的中点．
∴S_AEF=

3

8

，
∴VE-AB 1F=VB 1-AEF=

1

3

S_△AEF•B₁B=

1

3

×

3

8

×1=

1

8

．…（9分）
（Ⅲ）∵DE⊥平面AB₁F
∴∠EB₁D₁=α+β…（11分）
在△EB₁D₁中，B₁E=

5

2

，D₁E=

3

2

，B₁D₁=

2

．
∴os（α+β）=

B1E2+B1D12-D 1E2

2B1E•B1 D1

=

5 4 +2- 9 4

2× 5 2 × 2

=

10

10

．…（14分）

点评：本题主要考查线面垂直的证明以及线面所成的角的求法．在证明线面垂直时，一般先证明线线垂直，得到线面垂直．