
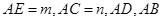 为方程
为方程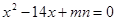 的两根,
的两根,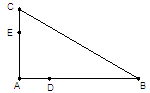
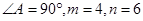 ,求C,B,D,E四点所在圆的半径。
,求C,B,D,E四点所在圆的半径。
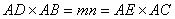
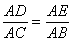 .又∠DAE=∠CAB,从而△ADE∽△ACB 因此∠ADE=∠ACB , 所以C,B,D,E四点共圆。
.又∠DAE=∠CAB,从而△ADE∽△ACB 因此∠ADE=∠ACB , 所以C,B,D,E四点共圆。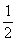 (12-2)=5.
(12-2)=5.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题

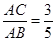 ,求
,求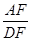 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
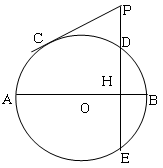
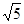 ,求PD的长.
,求PD的长.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
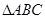 ,过顶点A的圆与边BC切于BC的中点P,与边AB、AC分别交于点M、N,且CN=2BM,点N平分AC.则
,过顶点A的圆与边BC切于BC的中点P,与边AB、AC分别交于点M、N,且CN=2BM,点N平分AC.则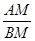 =( )
=( )
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
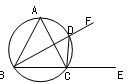
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com